 Giải bài tập Tài liệu Dạy - học Toán lớp 8, Phát triển tư duy đột phá trong dạy học Toán 8
Giải bài tập Tài liệu Dạy - học Toán lớp 8, Phát triển tư duy đột phá trong dạy học Toán 8
 Ôn tập chương 2 - Đa giác, diện tích đa giác
Ôn tập chương 2 - Đa giác, diện tích đa giác
Bài tập 4 trang 173 Tài liệu dạy – học Toán 8 tập 1
Giải bài tập a) Chứng minh rằng nếu một tam giác đều có cạnh bằng a thì diện tích bằng
Đề bài
a) Chứng minh rằng nếu một tam giác đều có cạnh bằng a thì diện tích bằng \({{{a^3}\sqrt 3 } \over 4}\) .
b) Tính diện tích của lục giác đều có cạnh bằng a.
Lời giải chi tiết
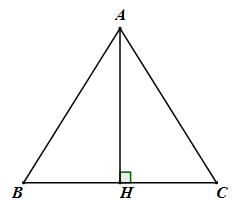
a) Kẻ AH là đường cao của tam giác ABC
\(\Delta ABC\) đều \( \Rightarrow AH\) là đường trung tuyến
\( \Rightarrow H\) là trung điểm của BC \( \Rightarrow BH = {{BC} \over 2} = {a \over 2}\)
\(\Delta ABH\) vuông tại H có \(A{H^2} + B{H^2} = A{B^2}\) (định lí Pytago)
\( \Rightarrow A{H^2} + {{{a^2}} \over 4} = {a^2} \Rightarrow A{H^2} = {{3{a^2}} \over 4} \Rightarrow AH = {{a\sqrt 3 } \over 2}\)
\({S_{ABC}} = {1 \over 2}AH.BC = {1 \over 2}.{{a\sqrt 3 } \over 2}.a = {{{a^2}\sqrt 3 } \over 4}\)
b)
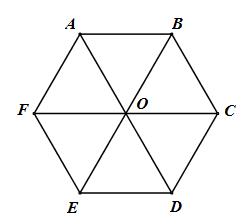
Gọi O là tâm của lục giác đều
Ta có : \({S_{ABCDEF}} = {S_{OAB}} + {S_{OBC}} + {S_{OCD}} + {S_{ODE}} + {S_{OEF}} + {S_{OAF}}\)
\({S_{OAB}} = {S_{OBC}} = {S_{OCD}} = {S_{ODE}} = {S_{OEF}} = {S_{OAF}}\)
(vì \(\Delta OAB = \Delta OBC = \Delta OCD = \Delta ODE = \Delta OEF = \Delta OAF\))
\( \Rightarrow {S_{ABCDEF}} = 6{S_{OAB}}\)
Mà \(\Delta OAB\) đều có cạnh bằng a, nên ta có \({S_{OAB}} = {{{a^2}\sqrt 3 } \over 4}\)
Do đó \({S_{ABCDEF}} = 6.{{{a^2}\sqrt 3 } \over 4} = {{3{a^2}\sqrt 3 } \over 2}\).
Loigiaihay.com












Danh sách bình luận