Bài tập 31 trang 93 Tài liệu dạy – học Toán 8 tập 2

Đề bài

Cho tam giác ABC vuông góc tại A (AB < AC), đường cao AH. Vẽ HM vuông góc với AC tại M.

a) Chứng minh rằng $A{H^2} = AM.AC$

b) Chứng minh rằng AM.AC = HB.HC.

c) Qua A vẽ đường thẳng song song với BC cắt đường thẳng HM tại I, vẽ In vuông góc với BC tại N. Chứng minh rằng $\Delta HMN \sim \Delta HCI$ .

d) Gọi E là giao điểm của IN với AC, HE cắt IC ở F, biết AB = 12 cm, BC = 20 cm. Tính diện tích tam giác AMF.

Lời giải chi tiết

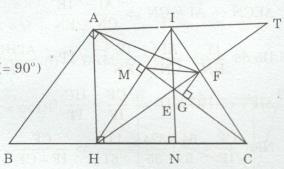
a) Xét ∆AHM và ∆AHC có: $\widehat {HAM}$ (chung) và $\widehat {AMH} = \widehat {AHC}( = 90^\circ )$

Do đó $\Delta AHM \sim \Delta ACH(g.g)$

$\Rightarrow {{AH} \over {AC}} = {{AM} \over {AH}} \Rightarrow A{H^2} = AM.AC(1)$

b) Xét ∆ABH và ∆AHC có: $\widehat {AHB} = \widehat {AHC}( = 90^\circ )$

Và $\widehat {BAH} = \widehat {ACH}$ (cùng phụ với góc B)

Do đó $\Delta ABH \sim \Delta CAH(g.g)$

$\Rightarrow {{AH} \over {CH}} = {{BH} \over {AH}} \Rightarrow A{H^2} = HB.HC(2)$

Từ (1) và (2) suy ra AM.AC = HB.HC

c) Xét ∆HMC và ∆HNI có: $\widehat {MHC}$ (chung) và $\widehat {HMC} = \widehat {HNI}( = 90^\circ )$

Do đó $\Delta HMC \sim \Delta HNI(g.g)$

$\Rightarrow {{HM} \over {HN}} = {{HC} \over {HI}}$

$\Rightarrow {{HM} \over {HC}} = {{HN} \over {HI}}$

Xét ∆HMN và ∆HCI có: $\widehat {IHC}$ (chung), ${{HM} \over {HC}} = {{HN} \over {HI}}$ (chứng minh trên)

Do đó $\Delta HMN \sim \Delta HCI(c.g.c)$

d) ∆ABC vuông tại A $\Rightarrow A{B^2} + A{C^2} = B{C^2}$ (định lí Py-ta-go)

Nên $AC = \sqrt {B{C^2} - A{B^2}}  = \sqrt {{{20}^2} - {{12}^2}}  = 16(cm)$

Ta có $AH.BC = AB.AC = ( = 2{S_{ABC}})$

$\Rightarrow AH = {{AB.AC} \over {BC}} = {{12.16} \over {20}} = {{48} \over 5}(cm)$

Mà $A{H^2} = AM.AC$ (câu a) nên $AM = {{A{H^2}} \over {AC}} = {\left( {{{48} \over 5}} \right)^2}:16 = {{144} \over {25}}(cm)$

$CM = AC - AM = 16 - {{144} \over {25}} = {{256} \over {25}}(cm)$

Ta có $AB \bot AC(gt),HM \bot AC(gt) \Rightarrow AB//HM$

Mà AI // BH (gt) => Tứ giác AIHB là hình bình hành

$\Rightarrow IH = AB = 12cm,AI = BH$

∆HAC vuông tại H $\Rightarrow A{H^2} + H{C^2} = A{C^2}$ (định lí Py-ta-go)

Do đó $HC = \sqrt {A{C^2} - A{H^2}}  = \sqrt {{{16}^2} - {{\left( {{{48} \over 5}} \right)}^2}}  = {{64} \over 5}(cm)$

Tứ giác AHNI là hình chữ nhật $\Rightarrow HN = AI = BH = BC - CH$$\,= 20 - {{64} \over 5} = {{36} \over 5}(cm)$

Nên $CN = CH - HN = {{64} \over 5} - {{36} \over 5} = {{28} \over 5}(cm)$

Gọi T là giao điểm của HF vafAI, vẽ $FG \bot AC$ tại G

∆EHN có IT // HN $\Rightarrow {{IT} \over {HN}} = {{IE} \over {EN}}$

∆ECN có AI // CN $\Rightarrow {{AI} \over {CN}} = {{IE} \over {EN}}$

Do đó ${{IT} \over {HN}} = {{AI} \over {CN}}\left( { = {{IE} \over {EN}}} \right)$

$\Rightarrow IT = {{AI.HN} \over {CN}} = \left( {{{36} \over 5}.{{36} \over 5}} \right):{{28} \over 5} = {{324} \over {35}}(cm)$

∆IFT có HC // IF $\Rightarrow {{CF} \over {IF}} = {{HC} \over {IT}}$

Nên ${{CF} \over {IF}} = {{64} \over 5}:{{324} \over {35}} = {{112} \over {81}}$

$\Rightarrow {{CF} \over {IF + CF}} = {{112} \over {81 + 112}}$

$\Rightarrow {{CF} \over {CI}} = {{112} \over {193}}$

∆MAI vuông tại M $\Rightarrow A{M^2} + I{M^2} = A{I^2}$ (định lí Py-ta-go)

Do đó $IM = \sqrt {A{I^2} - A{M^2}}$$\,= \sqrt {{{\left( {{{36} \over 5}} \right)}^2} - {{\left( {{{144} \over {25}}} \right)}^2}}  = {{108} \over {25}}(cm)$

Ta có $FG \bot AC,IM \bot AC \Rightarrow FG//IM$

∆GIM có FG // IM $\Rightarrow {{FG} \over {IM}} = {{CF} \over {CI}}$

$\Rightarrow FG = {{CF} \over {CI}}.IM$$\,= {{112} \over {193}}.{{108} \over {25}} = {{12096} \over {4825}}(cm)$

Do vậy ${S_{AMF}} = {1 \over 2}AM.FG$$\,= {1 \over 2}.{{144} \over {25}}.{{12096} \over {4825}} = {{870912} \over {120625}}(c{m^2})$

Loigiaihay.com