Giải bài tập Tài liệu Dạy - học Toán lớp 8, Phát triển tư duy đột phá trong dạy học Toán 8 Luyện tập - Chủ đề 2 : Tam giác đồng dạng và ứng dụng

Bài tập 26 trang 92 Tài liệu dạy – học Toán 8 tập 2


Giải bài tập Cho tam giác ABC vuông tại A (AB < AC). Kẻ đường cao AH. Tia phân giác của góc B cắt AC ở E, cắt AH ở F.

Đề bài

Cho tam giác ABC vuông tại A (AB < AC). Kẻ đường cao AH. Tia phân giác của góc B cắt AC ở E, cắt AH ở F.

a) Chứng minh rằng AB.HF = AE.HB.

b) Chứng minh rằng AE = AF.

c) Chứng minh rằng AE2 = EC.FH.

d) Cho biết AB = 9 cm, AC = 12 cm. Tính diện tích tam giác BHF.

Lời giải chi tiết

 

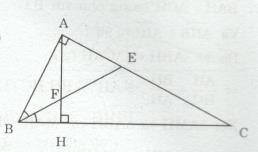
a) Xết ∆ABE và ∆BHF có:

\(\widehat {BAE} = \widehat {BHF}( = 90^\circ )\)

Và \(\widehat {ABE} = \widehat {FBH}\) (BE là tia phân giác của góc B)

Do đó \(\Delta ABE \sim \Delta HBF(g.g)\)

\( \Rightarrow {{AB} \over {HB}} = {{AE} \over {HF}} \Rightarrow AB.HF = AE.HB\)

b) Ta có \(\widehat {AEF} = \widehat {HFB}\) (vì \(\Delta ABE \sim \Delta HBF)\)

Và \(\widehat {HFB} = \widehat {AFE}\) (đối đỉnh)

\( \Rightarrow \widehat {AEF} = \widehat {AFE} \Rightarrow \Delta AEF\) cân tại A \( \Rightarrow AE = AF\)

c) Xét ∆ABH và ∆ABC có: góc B (chung) và \(\widehat {AHB} = \widehat {BAC}( = 90^\circ )\)

Do đó \(\Delta ABH \sim \Delta CBA(g.g) \)

\(\Rightarrow {{AB} \over {BC}} = {{BH} \over {AB}} \)

\(\Rightarrow {{BC} \over {AB}} = {{AB} \over {BH}}(1)\)

∆ABC có BE là đường phân giác (gt) nên \({{EC} \over {AE}} = {{BC} \over {AB}}(2)\)

∆ABH có BF là đường phân giác (gt) nên \({{AF} \over {FH}} = {{AB} \over {BH}}(3)\)

Từ (1), (2) và (3) suy ra: \({{EC} \over {AE}} = {{AF} \over {FH}} \Rightarrow AE.AF = EC.FH\)

Mà AF = AE (câu b) \( \Rightarrow AE.AE = EC.FH \Rightarrow A{E^2} = EC.FH\)
d) ∆ABC vuông tại A có \(B{C^2} = A{B^2} + A{C^2}\) (định lí Py-ta-go)

\( \Rightarrow B{C^2} = {9^2} + {12^2} = 225 \Rightarrow BC = 15(cm)\)

Ta có \(AH.BC = AB.AC( = 2{S_{ABC}}) \)

\(\Rightarrow AH = {{AB.AC} \over {BC}} = {{9.12} \over {15}} = 7,2(cm)\)

∆HAB vuông tại H \( \Rightarrow A{H^2} + B{H^2} = A{B^2}\) (định lý Py-ta-go)

Do đó \(B{H^2} = A{B^2} - A{H^2} = {9^2} - 7,{2^2} = 5,{4^2} \)

\(\Rightarrow BH = 5,4(cm)\)

∆ABH có BF là đường phân giác

\( \Rightarrow {{FH} \over {AF}} = {{BH} \over {AB}}\)

\(\Rightarrow {{FH} \over {BH}} = {{AF} \over {AB}} = {{FH + AF} \over {BH + AB}} = {{AH} \over {BH + AB}}\)

Nên \({{FH} \over {5,4}} = {{7,2} \over {5,4 + 9}} \)

\(\Rightarrow FH = 2,7(cm)\)

Do vậy \({S_{BHF}} = {1 \over 2}FH.BH = {1 \over 2}.2,7.5,4 = 7,29(c{m^2})\)

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store