-
CHƯƠNG 1: PHÉP NHÂN VÀ PHÉP CHIA ĐA THỨC
-
Chủ đề 1 : Phép nhân đa thức – Hằng đẳng thức đáng nhớ
-
Chủ đề 2 : Phân tích đa thức thành nhân tử
- 1. Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
- 2. Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
- 3. Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
- 4. Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp
- Bài tập - Chủ đề 2 : Phân tích đa thức thành nhân tử
- Luyện tập - Chủ đề 2 : Phân tích đa thức thành nhân tử
-
Chủ đề 3: Phép chia đa thức
-
Ôn tập chương 1 - Phép nhân và phép chia đa thức
-
-
CHƯƠNG 2: PHÂN THỨC ĐẠI SỐ
-
CHƯƠNG 1. TỨ GIÁC
-
Chủ đề 1 : Tứ giác – Hình thang
-
Chủ đề 2 : Hình bình hành – Hình chữ nhật – Hình thoi – Hình vuông
- 1. Đối xứng trục
- 2. Hình bình hành
- 3. Đối xứng tâm
- 4. Hình chữ nhật
- 5. Tập hợp các điểm cách đều một đường thẳng cho trước
- 6. Hình thoi
- 7. Hình vuông
- Bài tập - Chủ đề 2 : Hình bình hành – Hình chữ nhật – Hình thoi – Hình vuông
- Luyện tập - Chủ đề 2 : Hình bình hành – Hình chữ nhật – Hình thoi – Hình vuông
-
Ôn tập chương 1 - Tứ giác
-
-
CHƯƠNG 2. ĐA GIÁC. DIỆN TÍCH ĐA GIÁC
-
CHƯƠNG 3 : PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN – GIẢI BÀI TOÁN BẰNG CÁCH LẬP PHƯƠNG TRÌNH
-
CHƯƠNG 4. BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
-
CHƯƠNG 3. TAM GIÁC ĐỒNG DẠNG
-
Chủ đề 1 : Định lí Thales
-
Chủ đề 2 : Tam giác đồng dạng và ứng dụng
- 1. Khái niệm hai tam giác đồng dạng
- 2. Trường hợp đồng dạng thứ nhất (c.c.c)
- 3. Trường hợp đồng dạng thứ hai (c.g.c)
- 4. Trường hợp đồng dạng thứ ba (g.g)
- 5. Các trường hợp đồng dạng của tam giác vuông
- 6. Ứng dụng thực tế của tam giác đồng dạng
- Bài tập - Chủ đề 2 : Tam giác đồng dạng và ứng dụng
- Luyện tập - Chủ đề 2 : Tam giác đồng dạng và ứng dụng
-
-
CHƯƠNG 4 : HÌNH LĂNG TRỤ ĐỨNG – HÌNH CHÓP ĐỀU
-
ÔN TẬP CUỐI NĂM - TÀI LIỆU DẠY-HỌC TOÁN 8
Giải bài tập Tài liệu Dạy - học Toán lớp 8, Phát triển tư duy đột phá trong dạy học Toán 8
Luyện tập - Chủ đề 2 : Tam giác đồng dạng và ứng dụng
Bài tập 23 trang 92 Tài liệu dạy – học Toán 8 tập 2
Giải bài tập Cho tam giác ABC có ba góc nhọn, đường cao AH
Đề bài
Cho tam giác ABC có ba góc nhọn, đường cao AH \(\left( {H \in BC} \right)\). Vẽ \(HM \bot AB,\,\,HN \bot AC\,\,\)\(\left( {M \in AB,\,\,N \in AC} \right)\)
a) Chứng minh rằng \(\Delta AMH \sim \Delta AHB.\) Suy ra AH2 = AM.AB.
b) Chứng minh rằng AM.AB = AN.AC.
c) Chứng minh \(\Delta ANM \sim \Delta ABC.\)
d) Gọi O là giao điểm của AH với MN. Chứng minh OA.OH = OM.ON.
Lời giải chi tiết
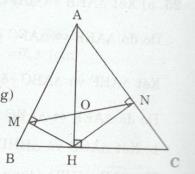
a) Xét ∆AMH và ∆AHB có: \(\widehat {MAH}\) chung và \(\widehat {AMH} = \widehat {AHB}( = 90^\circ )\)
Do đó \(\Delta AMH \sim \Delta AHB(g.g) \Rightarrow {{AH} \over {AB}} = {{AM} \over {AH}}\)
\( \Rightarrow A{H^2} = AM.AB(1)\)
b) Xét ∆AHN và ∆AHC có:
\(\widehat {HAN}\) chung và \(\widehat {ANH} = \widehat {AHC}( = 90^\circ )\)
\(\Rightarrow \Delta AHN \sim \Delta ACH(g.g)\)
\( \Rightarrow {{AH} \over {AC}} = {{AN} \over {AH}} \Rightarrow A{H^2} = AN.AC(2)\)
Từ (1) và (2) suy ra AM.AB = AN.AC
c) Xét ∆ANM và ∆ABC có: \({{AM} \over {AC}} = {{AN} \over {AB}}\) (vì AM.AB = AN.AC) và góc MAN (chung)
Do đó \(\Delta ANM \sim ABC(c.g.c)\)
d) Ta có \(\widehat {AMN} = \widehat {ACB}(\Delta ANM \sim \Delta ABC)\) và \(\widehat {AHN} = \widehat {ACB}(\Delta AHN \sim \Delta ACH)\)
\( \Rightarrow \widehat {AMN} = \widehat {AHN}\,hay\,\widehat {AMO} = \widehat {OHN}\)
Xét ∆AMO và ∆OHN có \(\widehat {AOM} = \widehat {NOH}\) (đối đỉnh) và \(\widehat {AMO} = \widehat {OHN}\)
Do đó \(\Delta AMO \sim \Delta NHO(g.g) \)
\(\Rightarrow {{OA} \over {ON}} = {{OM} \over {OH}}\)
\(\Rightarrow OA.OH = OM.ON\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài tập 24 trang 92 Tài liệu dạy – học Toán 8 tập 2
- Bài tập 25 trang 92 Tài liệu dạy – học Toán 8 tập 2
- Bài tập 26 trang 92 Tài liệu dạy – học Toán 8 tập 2
- Bài tập 27 trang 92 Tài liệu dạy – học Toán 8 tập 2
- Bài tập 28 trang 92 Tài liệu dạy – học Toán 8 tập 2
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
