Bài 52 trang 97 SBT toán 8 tập 2

Giải bài 52 trang 97 sách bài tập toán 8. Tứ giác ABCD có hai góc vuông tại đỉnh A và C, hai đường chéo AC và BD cắt nhau tại O ....

Đề bài

Tứ giác \(ABCD \) có hai góc vuông tại đỉnh \(A\) và \(C,\) hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(O,\) \(\widehat {BAO} = \widehat {BDC}\) (h.37)

Chứng minh:

a) \(∆ ABO\) đồng dạng \(∆ DCO\).

b) \(∆ BCO\) đồng dạng \(∆ ADO\).

Phương pháp giải - Xem chi tiết

Sử dụng: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.

Lời giải chi tiết

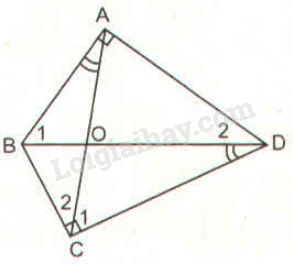
a) \(\widehat {BAO} = \widehat {BDC}\) (gt) hay \(\widehat {BAO} = \widehat {ODC}\)

Xét \( ∆ABO\) và \(∆ DCO\) có:

+) \(\widehat {BAO} = \widehat {ODC}\) (chứng minh trên)

+) \(\widehat {AOB} = \widehat {DOC}\) (đối đỉnh)

\( \Rightarrow ∆ ABO\) đồng dạng \(∆ DCO\) (g.g)

b) Vì \(∆ ABO\) đồng dạng \(∆ DCO\) nên \({\widehat B_1} = {\widehat C_1}\) (1)

Mà \({\widehat C_1} + {\widehat C_2} = \widehat {BCD} = 90^\circ \) (2)

Xét tam giác \(ABD\) có \(\widehat A = 90^\circ \) nên \({\widehat B_1} + {\widehat D_2} = 90^\circ \) (3)

Từ (1), (2) và (3) suy ra: \({\widehat C_2} = {\widehat D_2}\)

Xét \(∆ BCO\) và \(∆ ADO\) có:

\({\widehat C_2} = {\widehat D_2}\) (chứng minh trên )

\(\widehat {BOC} = \widehat {AOD}\) (đối đỉnh)

\( \Rightarrow ∆ BCO\) đồng dạng \(∆ ADO\) (g.g).

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.4 trên 18 phiếu

Bài tiếp theo

Bài 53 trang 97 SBT toán 8 tập 2
Giải bài 53 trang 97 sách bài tập toán 8. Cho hình chữ nhật ABCD có AB = a = 12 cm, BC = b = 9cm. Gọi H là chân đường vuông góc kẻ từ A xuống BD (h.38) ...
Bài 54 trang 97 SBT toán 8 tập 2
Giải bài 54 trang 97 sách bài tập toán 8. Tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O ...
Bài 55 trang 98 SBT toán 8 tập 2
Giải bài 55 trang 98 sách bài tập toán 8. Tam giác ABC có ba đường cao AD, BE, CF đồng quy tại H. Chứng minh rằng AH.DH = BH.EH = CH.FH.
Bài 56 trang 98 SBT toán 8 tập 2
Giải bài 56 trang 98 sách bài tập toán 8. Hai điểm M và K thứ tự nằm trên cạnh AB và BC của tam giác ABC; hai đoạn thẳng AK và CM cắt nhau tại điểm P...
Bài 57 trang 98 SBT toán 8 tập 2
Giải bài 57 trang 98 sách bài tập toán 8. Cho hình bình hành ABCD. Từ A kẻ AM vuông góc với BC, AN vuông góc với CD (M thuộc BC và N thuộc CD).
Bài 58 trang 98 SBT toán 8 tập 2
Giải bài 58 trang 98 sách bài tập toán 8. Giả sử AC là đường chéo lớn của hình bình hành ABCD. Từ C, vẽ đường vuông góc CE với đường thẳng AB ...
Bài 59 trang 98 SBT toán 8 tập 2
Giải bài 59 trang 98 sách bài tập toán 8. Tam giác ABC có hai đường cao là AD và BE (D thuộc BC, E thuộc AC)...
Bài 60 trang 98 SBT toán 8 tập 2
Giải bài 60 trang 98 sách bài tập toán 8. Tam giác ABC có hai trung tuyến AK và CL cắt nhau tại O. Từ một điểm P bất kì trên cạnh AC, vẽ các đường thẳng PE song song với AK ...
Bài 51 trang 97 SBT toán 8 tập 2
Giải bài 51 trang 97 sách bài tập toán 8. Cho tam giác ABC. a) Tìm trên cạnh AB điểm M sao cho AM/MB = 2/3 ...