Bài 51 trang 97 SBT toán 8 tập 2
Giải bài 51 trang 97 sách bài tập toán 8. Cho tam giác ABC. a) Tìm trên cạnh AB điểm M sao cho AM/MB = 2/3 ...
Đề bài
Cho tam giác \(ABC.\)
a) Tìm trên cạnh \(AB\) điểm \(M\) sao cho \(\displaystyle {{AM} \over {MB}} = {2 \over 3}\); tìm trên cạnh \(AC\) điểm \(N\) sao cho \(\displaystyle {{AN} \over {NC}} = {2 \over 3}\)
b) Vẽ đoạn thẳng \(MN.\) Hỏi rằng hai đường thẳng \(MN\) và \(BC\) có song song với nhau không? Vì sao?
c) Cho biết chu vi và diện tích tam giác \(ABC\) thứ tự là \(P\) và \(S.\) Tính chu vi và diện tích tam giác \(AMN.\)
Phương pháp giải - Xem chi tiết
Áp dụng định lí: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho.
Lời giải chi tiết
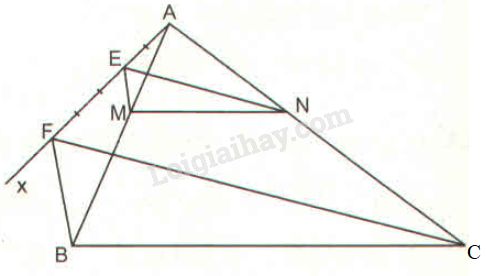
a) Cách vẽ:
- Kẻ tia \(Ax\) bất kì khác tia \(AB, AC.\)
- Trên tia \(Ax,\) lấy hai điểm \(E\) và \(F\) sao cho \(AE = 2 (cm), EF = 3 (cm).\)
- Kẻ đường thẳng \(FB.\)
- Từ \(E\) kẻ đường thẳng song song với \(FB\) cắt \(AB\) tại \( M\).
- Kẻ đường thẳng \(FC\)
- Từ \(E\) kẻ đường thẳng song song với \(FC\) cắt \(AC\) tại \(N\).
Ta được hai điểm \(M, N\) cần dựng.
Chứng minh:
Trong tam giác \(AFB\) có \(EM // FB\) (theo cách vẽ)
Theo định lí Ta-lét, ta có:
\(\displaystyle{{AM} \over {MB}} = {{AE} \over {EF}} = {2 \over 3}\)
Trong tam giác \(AFC\) có \(EN // FC\) (theo cách vẽ)
Theo định lí Ta-lét, ta có:
\(\displaystyle {{AN} \over {NC}} = {{AE} \over {EF}} = {2 \over 3}\)
Vậy \(M, N\) là hai điểm cần tìm.
b) Trong tam giác \(ABC\) có \(\displaystyle{{AM} \over {MB}} = {{AN} \over {NC}} = {2 \over 3}\) nên theo định lí đảo của định lí Ta-lét thì \(MN // BC.\)
c) Gọi \(p’\) và \(S’\) là chu vi và diện tích của \(∆ AMN\).
Ta có \(\displaystyle \dfrac{{AM}}{{MB}} = \dfrac{2}{3} \Rightarrow \dfrac{{AM}}{{AB}} = \dfrac{2}{5}\)
Trong tam giác \(ABC\) có \(MN // BC\) nên \(\dfrac{{AM}}{{AB}} = \dfrac{{AN}}{{AC}} = \dfrac{{MN}}{{BC}}\) hay \( ∆ AMN\) đồng dạng \(∆ ABC\) (c.c.c)
Với tỉ số đồng dạng: \( k=\dfrac{{AM}}{{AB}} = \dfrac{2}{5}\)
Ta có:
\(\dfrac{{AM}}{{AB}} = \dfrac{{AN}}{{AC}} = \dfrac{{MN}}{{BC}}\)\( = \dfrac{{AM + AN + MN}}{{AB + AC + BC}} = \dfrac{{p'}}{{{P}}}\)
Suy ra \(\displaystyle {{p'} \over P} = {2 \over 5} = k\Rightarrow p' = {2 \over 5}P \)
Theo tính chất hai tam giác đồng dạng ta có:
\(\displaystyle {{S'} \over S}=k^2 = {\left( {{2 \over 5}} \right)^2} = {4 \over 25} \)
\(\displaystyle\Rightarrow S' = {4 \over 25}S .\)
Loigiaihay.com













Danh sách bình luận