Bài 4.1, 4.2, 4.3, 4.4 phần bài tập bổ sung trang 54, 55 SBT toán 9 tập 2

Bài 4.1

Giải các phương trình sau bằng cách (chuyển các số hạng tự do sang vế phải; bằng công thức nghiệm) và so sánh kết quả tìm được:

a) \(4{x^2} - 9 = 0\)

b) \(5{x^2} + 20 = 0\)

c) \(2{x^2} - 2 + \sqrt 3  = 0\)

d) \(3{x^2} - 12 + \sqrt {145}  = 0\)

Phương pháp giải:

Cách 1: Chuyển các số hạng tự do sang vế phải, nhận xét vế trái và vế phải của phương trình để giải.

Chú ý: \({A^2} = B\,\,\left( {B \ge 0} \right) \Leftrightarrow |A| = \sqrt B \)

Cách 2: Phương trình \(a{x^2} + bx + c = 0(a \ne 0)\) và biệt thức \(\Delta  = {b^2} - 4ac\):

+) Nếu \(\Delta  > 0\) thì phương trình có hai nghiệm phân biệt:

\({x_1}\)= \(\dfrac{-b + \sqrt{\bigtriangleup }}{2a}\)  và \({x_2}\)= \(\dfrac{-b - \sqrt{\bigtriangleup }}{2a}\)

+) Nếu \(\Delta  = 0\) thì phương trình có nghiệm kép \({x_1}={x_2}=\dfrac{-b }{2a}\).

+) Nếu \(\Delta  < 0\) thì phương trình vô nghiệm.

Lời giải chi tiết:

a) Cách 1:

\(4{x^2} - 9 = 0 \) 

\(\Leftrightarrow 4{x^2} = 9 \)

\( \displaystyle \Leftrightarrow {x^2} = {9 \over 4} \)

\(\displaystyle\Leftrightarrow x = \pm {3 \over 2}  \)

Phương trình có hai nghiệm là: \(\displaystyle {x_1} = {3 \over 2};{x_2} =  - {3 \over 2}\)

Cách 2:

\(\eqalign{
& \Delta = {0^2} - 4.4.\left( { - 9} \right) = 144 > 0 \cr 
& \sqrt \Delta = \sqrt {144} = 12 \cr 
& {x_1} = {{0 + 12} \over {2.4}} = {{12} \over 8} = {3 \over 2} \cr 
& {x_2} = {{0 - 12} \over {2.4}} = {{ - 12} \over 8} = - {3 \over 2} \cr} \)

Vậy hai cách giải ta nhận được kết quả nghiệm giống nhau.

b) Cách 1:

\(5{x^2} + 20 = 0 \Leftrightarrow 5{x^2} =  - 20\)

Vế trái \(5{x^2} \ge 0\); vế phải \(-20 < 0\)

Do đó không có giá trị nào của \(x\) để \(5{x^2} =  - 20\)

Phương trình vô nghiệm.

Cách 2:

\(\Delta  = {0^2} - 4.5.20 =  - 400 < 0.\) Phương trình vô nghiệm.

Vậy hai cách giải ta nhận được kết quả nghiệm giống nhau.

c) Cách 1:

\(2{x^2} - 2 + \sqrt 3 = 0 \)

\( \Leftrightarrow 2{x^2} = 2 - \sqrt 3 \)

\(\Leftrightarrow \displaystyle{x^2} = {{2 - \sqrt 3 } \over 2} \)

\(\displaystyle \Leftrightarrow \left| x \right| = \sqrt {{{2 - \sqrt 3 } \over 2}} = \sqrt {{{4 - 2\sqrt 3 } \over 4}} \)

\(\displaystyle \Leftrightarrow \left| x \right| = {{\sqrt {4 - 2\sqrt 3 } } \over 2} \)\(\,\displaystyle= {{\sqrt {{{\left( {\sqrt 3 - 1} \right)}^2}} } \over 2} \)

\(\displaystyle\Leftrightarrow \left| x \right|= {{\sqrt 3 - 1} \over 2}  \)

\( \Leftrightarrow \left[ \begin{array}{l}
{x_1} = \dfrac{{\sqrt 3 - 1}}{2}\\
{x_2} = \dfrac{{1 - \sqrt 3 }}{2}
\end{array} \right.\)

Phương trình có hai nghiệm là:

\(\displaystyle {x_1} = {{\sqrt 3  - 1} \over 2};{x_2}  = {{1 - \sqrt 3 } \over 2}\)

Cách 2:

\( \Delta = {0^2} - 4.2\left( { - 2 + \sqrt 3 } \right) \)\(\,= 16 - 8\sqrt 3 \)

\(= 4\left( {4 - 2\sqrt 3 } \right) = 4{\left( {\sqrt 3 - 1} \right)^2} > 0 \)

\( \sqrt \Delta = \sqrt {4{{\left( {\sqrt 3 - 1} \right)}^2}} = 2\left( {\sqrt 3 - 1} \right) \)

Phương trình có hai nghiệm phân biệt là:

\( \displaystyle {x_1} = {{0 + 2\left( {\sqrt 3 - 1} \right)} \over {2.2}} = {{\sqrt 3 - 1} \over 2} \)

\( \displaystyle {x_2} = {{0 - 2\left( {\sqrt 3 - 1} \right)} \over {2.2}}\)\(\,\displaystyle = {{ - \left( {\sqrt 3 - 1} \right)} \over 2}\)\(\, \displaystyle = {{1 - \sqrt 3 } \over 2}  \)

Vậy hai cách giải ta nhận được kết quả nghiệm giống nhau.

d) Cách 1:

\(\eqalign{
& 3{x^2} - 12 + \sqrt {145} = 0 \cr 
& \Leftrightarrow 3{x^2} = 12 - \sqrt {145} \cr 
& \Leftrightarrow {x^2} = {{12 - \sqrt {145} } \over 3} \cr} \)

Vì \(12 = \sqrt {144} ;\sqrt {144}  < \sqrt {145}\)

\( \displaystyle \Rightarrow {{12 - \sqrt {145} } \over 3} < 0\)

Ta có vế trái \({x^2} \ge 0\), vế phải \( \displaystyle {{12 - \sqrt {145} } \over 3} < 0\)

Phương trình vô nghiệm.

Cách 2:

\(\Delta  = {0^2} - 4.3\left( { - 12 + \sqrt {145} } \right) \)\(\,=  - 12\left( {\sqrt {145}  - 12} \right)\)

Vì \(\sqrt {145}  - 12 > 0 \) \(\Rightarrow  - 12\left( {\sqrt {145}  - 12} \right) < 0\)

\( \Rightarrow \Delta  < 0.\)

Phương trình vô nghiệm.

Vậy hai cách giải ta nhận được kết quả nghiệm giống nhau.

Bài 4.2

Giải các phương trình sau bằng hai cách (giải phương trình tích; bằng công thức nghiệm) và so sánh kết quả tìm được:

a) \(5{x^2} - 3x = 0\)

b) \(3\sqrt 5 {x^2} + 6x = 0\)

c) \(2{x^2} + 7x = 0\)

d) \(2{x^2} - \sqrt 2 x = 0\)

Phương pháp giải:

Cách 1: Đưa phương trình đã cho về dạng phương trình tích:

\(A\left( x \right).B\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}
A\left( x \right) = 0\\
B\left( x \right) = 0
\end{array} \right.\)

Cách 2: Phương trình \(a{x^2} + bx + c = 0(a \ne 0)\) và biệt thức \(\Delta  = {b^2} - 4ac\):

+) Nếu \(\Delta  > 0\) thì phương trình có hai nghiệm phân biệt:

\({x_1}\)= \(\dfrac{-b + \sqrt{\bigtriangleup }}{2a}\)  và \({x_2}\)= \(\dfrac{-b - \sqrt{\bigtriangleup }}{2a}\)

+) Nếu \(\Delta  = 0\) thì phương trình có nghiệm kép \({x_1}={x_2}=\dfrac{-b }{2a}\).

+) Nếu \(\Delta  < 0\) thì phương trình vô nghiệm.

Lời giải chi tiết:

a) Cách 1:

\( 5{x^2} - 3x = 0 \)

\( \Leftrightarrow x\left( {5x - 3} \right) = 0  \)

\(⇔ x = 0\) hoặc \(5x - 3 =0\)

\(⇔ x = 0\) hoặc \(\displaystyle x = {3 \over 5}.\)

Vậy phương trình có hai nghiệm là: \({x_1} = 0;{x_2} =\displaystyle {3 \over 5}\).

Cách 2:

\(\eqalign{
& \Delta = {\left( { - 3} \right)^2} - 4.5.0 = 9 > 0 \cr 
& \sqrt \Delta = \sqrt 9 = 3 \cr 
& {x_1} = {{3 + 3} \over {2.5}} = {6 \over {10}} = {3 \over 5} \cr 
& {x_2} = {{3 - 3} \over {2.5}} = {0 \over {10}} = 0 \cr} \)

Vậy phương trình có hai nghiệm là: \({x_1} = 0;{x_2} =\displaystyle {3 \over 5}\).

Nhận xét: Hai cách giải đều có kết quả nghiệm giống nhau.

b) Cách 1:

\( 3\sqrt 5 {x^2} + 6x = 0 \)

\( \Leftrightarrow 3x\left( {\sqrt 5 x + 2} \right) = 0  \)

\(⇔ x = 0\) hoặc \(\sqrt 5 x + 2 = 0\)

\(⇔ x = 0\) hoặc \(\displaystyle x =  - {{2\sqrt 5 } \over 5}\)

Vậy phương trình có hai nghiệm \(\displaystyle {x_1} = 0;{x_2} =  - {{2\sqrt 5 } \over 5}\).

Cách 2:

\(\eqalign{
& \Delta = {6^2} - 4.3\sqrt 5 .0 = 36 > 0 \cr 
& \sqrt \Delta = \sqrt {36} = 6 \cr 
& {x_1} = {{ - 6 + 6} \over {2.3\sqrt 5 }} = {0 \over {6\sqrt 5 }} = 0 \cr 
& {x_2} = {{ - 6 - 6} \over {2.3\sqrt 5 }} = {{ - 12} \over {6\sqrt 5 }} = - {{2\sqrt 5 } \over 5} \cr} \)

Vậy phương trình có hai nghiệm \(\displaystyle {x_1} = 0;{x_2} =  - {{2\sqrt 5 } \over 5}\).

Nhận xét: Hai cách giải đều có kết quả nghiệm giống nhau.

c) Cách 1:

\(2{x^2} + 7x = 0 \)

\( \Leftrightarrow x\left( {2x + 7} \right) = 0  \)

\(⇔ x = 0\) hoặc \(2x + 7 = 0\)

\(⇔ x = 0\) hoặc \(\displaystyle x =  - {7 \over 2}\)

Vậy phương trình có hai nghiệm \({x_1} = 0;\displaystyle {x_2} =  - {7 \over 2}\)

Cách 2:

\(\eqalign{
& \Delta = {7^2} - 4.2.0 = 49 > 0 \cr 
& \sqrt \Delta = \sqrt {49} = 7 \cr 
& {x_1} = {{ - 7 + 7} \over {2.2}} = {0 \over 4} = 0 \cr 
& {x_2} = {{ - 7 - 7} \over {2.2}} = {{ - 14} \over 4} = - {7 \over 2} \cr} \)

Vậy phương trình có hai nghiệm \({x_1} = 0;\displaystyle {x_2} =  - {7 \over 2}\)

Nhận xét: Hai cách giải đều có kết quả nghiệm giống nhau.

d) Cách 1:

\( 2{x^2} - \sqrt 2 x = 0 \)

\(\Leftrightarrow x\left( {2x - \sqrt 2 } \right) = 0 \)

\(⇔ x = 0\) hoặc \(2x - \sqrt 2  = 0\)

\(⇔ x = 0\) hoặc \(\displaystyle x = {{\sqrt 2 } \over 2}\)

Vậy phương trình có hai nghiệm \( x _1= 0;\,\displaystyle x = {{\sqrt 2 } \over 2}\).

Cách 2:

\(\eqalign{
& \Delta = {\left( { - \sqrt 2 } \right)^2} - 4.2.0 = 2 > 0 \cr 
& \sqrt \Delta = \sqrt 2 \cr 
& {x_1} = {{\sqrt 2 + \sqrt 2 } \over {2.2}} = {{2\sqrt 2 } \over 4} = {{\sqrt 2 } \over 2} \cr 
& {x_2} = {{\sqrt 2 - \sqrt 2 } \over {2.2}} = {0 \over 4} = 0 \cr} \)

Vậy phương trình có hai nghiệm \( x _1= 0;\,\displaystyle x = {{\sqrt 2 } \over 2}\).

Nhận xét: Hai cách giải đều có kết quả nghiệm giống nhau.

Bài 4.3

Giải các phương trình:

a) \({x^2} = 14 - 5x\)

b) \(3{x^2} + 5x = {x^2} + 7x - 2\)

c) \({\left( {x + 2} \right)^2} = 3131 - 2x\)

d) \(\displaystyle {{{{\left( {x + 3} \right)}^2}} \over 5} + 1 = {{{{\left( {3x - 1} \right)}^2}} \over 5} \)\(\,\displaystyle+ {{x\left( {2x - 3} \right)} \over 2}\)

Phương pháp giải:

Phương trình \(a{x^2} + bx + c = 0(a \ne 0)\) và biệt thức \(\Delta  = {b^2} - 4ac\):

+) Nếu \(\Delta  > 0\) thì phương trình có hai nghiệm phân biệt:

\({x_1}\)= \(\dfrac{-b + \sqrt{\bigtriangleup }}{2a}\)  và \({x_2}\)= \(\dfrac{-b - \sqrt{\bigtriangleup }}{2a}\)

+) Nếu \(\Delta  = 0\) thì phương trình có nghiệm kép \({x_1}={x_2}=\dfrac{-b }{2a}\).

+) Nếu \(\Delta  < 0\) thì phương trình vô nghiệm.

Lời giải chi tiết:

a) \({x^2} = 14 - 5x \)

\(\Leftrightarrow {x^2} + 5x - 14 = 0\)

\( \Delta = {5^2} - 4.1.\left( { - 14} \right) \)\(\,= 25 + 56 = 81 > 0 \)

\( \sqrt \Delta = \sqrt {81} = 9 \)

Phương trình có hai nghiệm phân biệt là:

\(\displaystyle  {x_1} = {{ - 5 + 9} \over {2.1}} = {4 \over 2} = 2 \) 

\( \displaystyle {x_2} = {{ - 5 - 9} \over {2.1}} = {{ - 14} \over 2} = - 7  \)

b) \(3{x^2} + 5x = {x^2} + 7x - 2 = 0 \)

\( \Leftrightarrow 2{x^2} - 2x + 2 = 0\)

\(\Leftrightarrow {x^2} - x + 1 = 0 \)

\( \Delta = {\left( { - 1} \right)^2} - 4.1.1 = 1 - 4 = - 3 < 0 \)

Phương trình vô nghiệm.

c) \( {\left( {x + 2} \right)^2} = 3131 - 2x \)

\( \Leftrightarrow {x^2} + 4x + 4 + 2x - 3131 = 0 \)

\( \Leftrightarrow {x^2} + 6x - 3127 = 0 \)

\( \Delta = {6^2} - 4.1.\left( { - 3127} \right) \)\(\,= 36 + 12508 = 12544 > 0 \)

\(\sqrt \Delta = \sqrt {12544} = 112 \)

Phương trình có hai nghiệm phân biệt là:

\( \displaystyle {x_1} = {{ - 6 + 112} \over {2.1}} = {{106} \over 2} = 53 \)

\( \displaystyle {x_2} = {{ - 6 - 112} \over {2.1}} = - 59 \)

d) \(\displaystyle {{{{\left( {x + 3} \right)}^2}} \over 5} + 1 = {{{{\left( {3x - 1} \right)}^2}} \over 5} \) \(\displaystyle + {{x\left( {2x - 3} \right)} \over 2} \)

\(\displaystyle \Leftrightarrow 2{\left( {x + 3} \right)^2} + 10 = 2{\left( {3x - 1} \right)^2} \) \(+ 5x\left( {2x - 3} \right) \)

\(\Leftrightarrow 2{x^2} + 12x + 18 + 10 = 18{x^2} - 12x \)\(\,+ 2 + 10{x^2} - 15x \)

\( \Leftrightarrow 26{x^2} - 39x - 26 = 0 \)

\( \Leftrightarrow 2{x^2} - 3x - 2 = 0 \)

\(\Delta = {\left( { - 3} \right)^2} - 4.2.\left( { - 2} \right) = 9 + 16\)\(\, = 25 > 0 \)

\(\sqrt \Delta = \sqrt {25} = 5 \)

Phương trình có hai nghiệm phân biệt là:

\(\displaystyle {x_1} = {{3 + 5} \over {2.2}} = {8 \over 4} = 2 \)

\(\displaystyle {x_2} = {{3 - 5} \over {2.2}} = - {1 \over 2} \)

Bài 4.4

Chứng minh rằng nếu phương trình \(a{x^2} + bx + c = x(a \ne 0)\) vô nghiệm thì phương trình \(a{\left( {a{x^2} + bx + c} \right)^2} + b\left( {a{x^2} + bx + c} \right)\)\(\, + c = x\) cũng vô nghiệm.

Phương pháp giải:

Cho phương trình \(a{x^2} + bx + c = 0\;(a \ne 0)\) và biệt thức \(\Delta  = {b^2} - 4ac\):

Phương trình vô nghiệm khi và chỉ khi \(\Delta  < 0\).

Lời giải chi tiết:

Phương trình \(a{x^2} + bx + c = x\;(a \ne 0)\) vô nghiệm.

\( \Leftrightarrow  a{x^2} + \left( {b - 1} \right)x + c = 0\) vô nghiệm

\(\eqalign{
& \Rightarrow \Delta = {\left( {b - 1} \right)^2} - 4ac < 0\cr 
& \Leftrightarrow 4ac - {\left( {b - 1} \right)^2} > 0 \cr} \)

Đặt \(f\left( x \right) =a{x^2} + bx + c\)

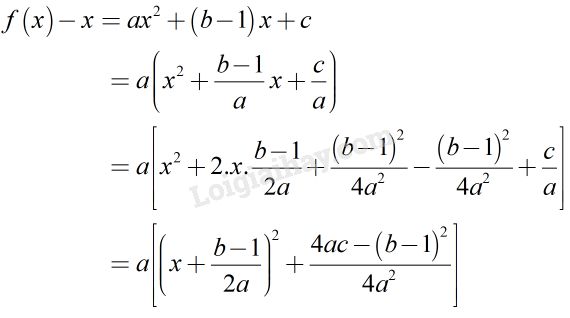
Vì \(\displaystyle{\left( {x + {{b - 1} \over {2a}}} \right)^2}\ge0\) và \(4ac - {\left( {b - 1} \right)^2} > 0\)

Do đó \(\displaystyle {\left( {x + {{b - 1} \over {2a}}} \right)^2} + {{4ac - {{\left( {b - 1} \right)}^2}} \over {4{a^2}}} > 0 \)

\(\Rightarrow f\left( x \right) - x\) luôn cùng dấu với \(a.\)

- Nếu \(a > 0\) thì \( f\left( x \right) - x > 0 \) \(\Rightarrow f\left( x \right) > x\) với mọi \(x.\)

Suy ra: \(a{\left[ {f\left( x \right)} \right]^2} + bf\left( x \right) + c > f\left( x \right) > x\) với mọi \(x.\)

Vậy không có giá trị nào của \(x\) để \(a{\left[ {f\left( x \right)} \right]^2} + bf\left( x \right) + c = x\)

- Nếu \(a < 0\) thì \(  f\left( x \right) - x < 0 \Leftrightarrow f\left( x \right) < x\) với mọi \(x\)

Suy ra: \(a{\left[ {f\left( x \right)} \right]^2} + bf\left( x \right) + c < f\left( x \right) < x\) với mọi \(x.\)

Vậy không có giá trị nào của \(x\) để  \(a{\left[ {f\left( x \right)} \right]^2} + bf\left( x \right) + c = x\)

Vậy phương trình \(a{\left( {a{x^2} + bx + c} \right)^2} + b\left( {a{x^2} + bx + c} \right)\)\(\, + c = x\) vô nghiệm.

Loigiaihay.com