Bài 31 trang 160 SBT toán 8 tập 1

Giải bài 31 trang 160 sách bài tập toán 8. Các điểm E, F, G, H, K, L, M, N chia mỗi cạnh hình vuông ABCD thành ba đoạn thẳng bằng nhau. Gọi P, Q, R, S là giao điểm của EH và NK với FM và GL (h.187). Tính...

Đề bài

Các điểm \(E, F, G, H, K, L, M, N\) chia mỗi cạnh hình vuông \(ABCD\) thành ba đoạn thẳng bằng nhau. Gọi \(P, Q, R, S\) là giao điểm của \(EH\) và \(NK\) với \(FM\) và \(GL\) (h.187). Tính diện tích của ngũ giác \(AEPSN\) và của tứ giác \(PQRS,\) biết \(AB = 6cm.\)

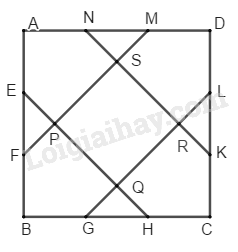
Phương pháp giải - Xem chi tiết

Biết diện tích hai tam giác vuông \(EBH\) và \(NDK\) thì tính được diện tích còn lại. Diện tích còn lại được chia thành năm phần bằng nhau, từ đó diện tích ngũ giác là một phần rưỡi và diện tích của tứ giác là hai phần.

Lời giải chi tiết

Diện tích hình vuông \(ABCD\) bằng \( 6.6=36\) (\(c{m^2}\))

Diện tích tam giác \(DKN\) bằng:

\(\dfrac{1}{2}.4.4 = 8\) (\(c{m^2}\))

Diện tích tam giác \(EBH\) bằng: \(\dfrac{1}{2}.4.4 = 8\) (\(c{m^2}\))

Diện tích phần còn lại là : \(36 – ( 8 + 8) = 20\) (\(c{m^2}\))

Trong tam giác vuông \(AEN\), theo định lý Pytago ta có:

\(E{N^2} = A{N^2} + A{E^2}\) \(= 4 + 4 = 8\)

\(EN =\) \(2\sqrt 2 \) \((cm)\)

Trong tam giác vuông \(BHE\), theo định lý Pytago ta có:

\(E{H^2} = B{E^2} + B{H^2}\) \(= 16 + 16 = 32\)

\(EH =\) \(4\sqrt 2 \) \((cm)\)

Diện tích hình chữ nhật \(ENKH\) bằng \(2\sqrt 2\, .\) \(4\sqrt 2 \) \(=16\) (\(c{m^2}\))

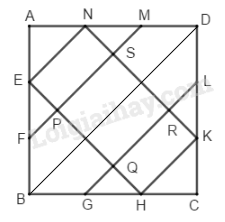
Nối đường chéo \(BD.\) Théo tính chất đường thẳng song song cách đều ta có hình chữ nhật \(ENKH\) được chia thành \(4\) phần bằng nhau nên diện tích tứ giác \(PQRS\) chiếm \(2\) phần và bằng 8 \(c{m^2}\)

Diện tích \(ΔAEN\) bằng \(\dfrac{1}{2}.2.2 = 2\left( {c{m^2}} \right)\)

Vậy \({S_{AEPSN}} = {S_{AEN}} + {S_{EPSN}}\)

\(= 2 + \dfrac{16}{4} = 6\) (\(c{m^2}\))

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.4 trên 5 phiếu

Bài tiếp theo

Bài 3.1 phần bài tập bổ sung trang 160 SBT toán 8 tập 1
Giải bài 3.1 phần bài tập bổ sung trang 160 sách bài tập toán 8 tập 1. a) Có thể dùng kéo cắt hai lần và chỉ cắt theo đường thẳng chia một tam giác (thường) thành ba mảnh để ghép lại được một hình chữ nhật hay không ?
Bài 3.2 phần bài tập bổ sung trang 161 SBT toán 8 tập 1
Giải bài 3.2 phần bài tập bổ sung trang 161 sách bài tập toán 8. Cho tam giác đều ABC và điểm M bất kì nằm trong tam giác đó. Đường thẳng đi qua điểm M và vuông góc với BC tại điểm H...
Bài 3.3 phần bài tập bổ sung trang 161 SBT toán 8 tập 1
Giải bài 3.3 phần bài tập bổ sung trang 161 sách bái tập toán 8. Cho hai tam giác ABC và DBC. Kẻ đường cao AH của tam giác ABC. Kẻ đường cao DK của tam giác DBC. Gọi S là diện tích của tam giác ABC...
Bài 30 trang 160 SBT toán 8 tập 1
Giải bài 30 trang 160 sách bài tập toán 8. Cho tam giác ABC, biết AB = 3AC. Tính tỉ số hai đường cao xuất phát từ các đỉnh B và C.
Bài 29 trang 160 SBT toán 8 tập 1
Giải bài 29 trang 160 sách bài tập toán 8. Hai cạnh của một tam giác có độ dài là 5cm và 6cm. Hỏi diện tích của tam giác đó có thể lấy giá trị nào trong các giá trị sau:
Bài 28 trang 160 SBT toán 8 tập 1
Giải bài 28 trang 160 sách bài tập toán 8. Tính diện tích của hình 186 theo các kích thước đã cho trên hình (a, b, c có cùng đơn vị đo).
Bài 27 trang 159 SBT toán 8 tập 1
Giải bài 27 trang 159 sách bài tập toán 8. Tam giác ABC có đáy BC cố định và dài 4cm. Đỉnh A di chuyển trên đường thẳng d (d ⊥ BC). Gọi H là chân đường cao hạ từ đỉnh A xuống đường thẳng BC.
Bài 26 trang 159 SBT toán 8 tập 1
Giải bài 26 trang 159 sách bài tập toán 8. Cho tam giác ABC có đáy BC cố định và đỉnh A di động trên một đường thẳng d cố định song song với đường thẳng BC. Chứng minh rằng tam giác ABC luôn có diện tích không đổi.
Bài 25 trang 159 SBT toán 8 tập 1
Giải bài 25 trang 159 sách bài tập toán 8. Hai đường chéo của hình chữ nhật chia hình chữ nhật thành bốn tam giác. Diện tích của các tam giác đó có bằng nhau không ? Vì sao ?