-
PHẦN ĐẠI SỐ - SBT TOÁN 8 TẬP 1
-
CHƯƠNG 1: PHÉP NHÂN VÀ PHÉP CHIA CÁC ĐA THỨC
- Bài 1. Nhân đơn thức với đa thức
- Bài 2. Nhân đa thức với đa thức
- Bài 3, 4, 5. Những hằng đẳng thức đáng nhớ
- Bài 6. Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
- Bài 7. Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
- Bài 8. Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
- Bài 9. Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp
- Bài 10. Chia đơn thức cho đơn thức
- Bài 11. Chia đa thức cho đơn thức
- Bài 12. Chia đa thức một biến đã sắp xếp
- Bài tập ôn chương 1 - Phép nhân và phép chia các đa thức
-
CHƯƠNG 2: PHÂN THỨC ĐẠI SỐ
- Bài 1. Phân thức đại số
- Bài 2. Tính chất cơ bản của phân thức
- Bài 3. Rút gọn phân thức
- Bài 4. Quy đồng mẫu thức nhiều phân thức
- Bài 5. Phép cộng các phân thức đại số
- Bài 6. Phép trừ các phân thức đại số
- Bài 7. Phép nhân các phân thức đại số
- Bài 8. Phép chia các phân thức đại số
- Bài 9. Biến đổi các biểu thức hữu tỉ. Giá trị của phân thức
- Bài tập ôn chương 2 - Phân thức đại số
-
-
PHẦN HÌNH HỌC - SBT TOÁN 8 TẬP 1
-
CHƯƠNG 1: TỨ GIÁC
- Bài 1. Tứ giác
- Bài 2. Hình thang
- Bài 3. Hình thang cân
- Bài 4. Đường trung bình của tam giác, của hình thang
- Bài 5. Dựng hình bằng thước và compa. Dựng hình thang
- Bài 6. Đối xứng trục
- Bài 7. Hình bình hành
- Bài 8. Đối xứng tâm
- Bài 9. Hình chữ nhật
- Bài 10. Đường thẳng song song với một đường thẳng cho trước
- Bài 11. Hình thoi
- Bài 12. Hình vuông
- Bài tập ôn chương 1 - Tứ giác
-
CHƯƠNG 2: ĐA GIÁC - DIỆN TÍCH ĐA GIÁC
-
-
PHẦN ĐẠI SỐ - SBT TOÁN 8 TẬP 2
-
PHẦN HÌNH HỌC - SBT TOÁN 8 TẬP 2
-
CHƯƠNG 3: TAM GIÁC ĐỒNG DẠNG
- Bài 1. Định lí Ta-lét trong tam giác
- Bài 2. Định lí đảo và hệ quả của định lí Ta-lét
- Bài 3. Tính chất đường phân giác của tam giác
- Bài 4. Khái niệm hai tam giác đồng dạng
- Bài 5. Trường hợp đồng dạng thứ nhất (c.c.c)
- Bài 6. Trường hợp đồng dạng thứ hai (c.g.c)
- Bài 7. Trường hợp đồng dạng thứ ba (g.g)
- Bài 8. Các trường hợp đồng dạng của tam giác vuông
- Ôn tập chương 3 - Tam giác đồng dạng
-
CHƯƠNG 4: HÌNH LĂNG TRỤ ĐỨNG. HÌNH CHÓP ĐỀU
- Bài 1. Hình hộp chữ nhật
- Bài 2. Hình hộp chữ nhật (tiếp)
- Bài 3. Thể tích của hình hộp chữ nhật
- Bài 4. Hình lăng trụ đứng
- Bài 5. Diện tích xung quanh của hình lăng trụ đứng
- Bài 6. Thể tích của hình lăng trụ đứng
- Bài 7. Hình chóp đều và hình chóp cụt đều
- Bài 8. Diện tích xung quanh của hình chóp đều
- Bài 9. Thể tích của hình chóp đều
- Ôn tập chương 4 - Hình lăng trụ đứng. Hình chóp đều
-
ÔN TẬP CUỐI NĂM
-
Bài 30 trang 160 SBT toán 8 tập 1
Giải bài 30 trang 160 sách bài tập toán 8. Cho tam giác ABC, biết AB = 3AC. Tính tỉ số hai đường cao xuất phát từ các đỉnh B và C.
Đề bài
Cho tam giác \(ABC,\) biết \(AB = 3AC.\) Tính tỉ số hai đường cao xuất phát từ các đỉnh \(B\) và \(C.\)
Phương pháp giải - Xem chi tiết
Áp dụng công thức tính diện tích tam giác: \(S=\dfrac{1}{2}ah\) với \(h;a\) lần lượt là độ dài chiều cao và cạnh đáy tương ứng.
Lời giải chi tiết
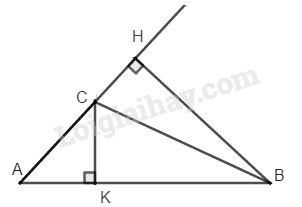
Trong tam giác \(ABC\) kẻ đường cao \(BH\) và \(CK\)
Ta có: \({S_{ABC}} = \dfrac {1}{2}AB.CK = \dfrac {1}{2}AC.BH\)
Suy ra: \(AB.CK = AC.BH\)
\( \Rightarrow \dfrac {BH}{CK} = \dfrac {AB}{AC}\)
Mà \(AB = 3 AC\) (gt) \( \Rightarrow \dfrac {BH}{CK} = \dfrac {3AC}{AC} = 3\)
Vậy đường cao \(BH\) dài gấp \(3\) lần đường cao \(CK.\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 31 trang 160 SBT toán 8 tập 1
- Bài 3.1 phần bài tập bổ sung trang 160 SBT toán 8 tập 1
- Bài 3.2 phần bài tập bổ sung trang 161 SBT toán 8 tập 1
- Bài 3.3 phần bài tập bổ sung trang 161 SBT toán 8 tập 1
- Bài 29 trang 160 SBT toán 8 tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
