Bài 26 trang 160 SBT toán 9 tập 1

Giải bài 26 trang 160 sách bài tập toán 9. Cho đường tròn (O), dây AB và dây CD, AB < CD. Giao điểm K của các đường thẳng AB, CD nằm ngoài đường tròn. Đường tròn (O ; OK) cắt KA và KC tại M và N. Chứng minh rằng KM < KN.

Đề bài

Cho đường tròn \((O),\) dây \(AB\) và dây \(CD,\) \(AB < CD.\) Giao điểm \(K\) của các đường thẳng \(AB,\) \(CD\) nằm ngoài đường tròn. Đường tròn \((O ; OK)\) cắt \(KA\) và \(KC\) tại \(M\) và \(N.\) Chứng minh rằng \(KM < KN.\)

Phương pháp giải - Xem chi tiết

Sử dụng kiến thức: Trong hai dây của một đường tròn:

+) Dây nào lớn hơn thì dây đó gần tâm hơn.

+) Dây nào gần tâm hơn thì dây đó lớn hơn.

Lời giải chi tiết

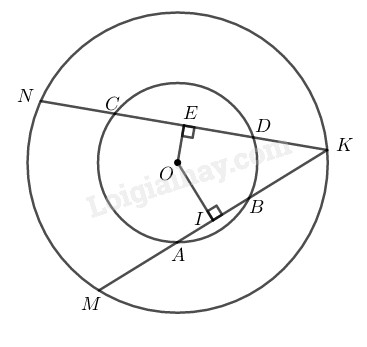
Kẻ \(OI ⊥ AB,\) \(OE ⊥ CD\)

Trong \(( O ; OA)\) ta có: \(AB < CD\;\; (gt)\)

Suy ra: \(OI > OE\) (dây lớn hơn gần tâm hơn)

Trong \((O ; OK)\) ta có: \(OI > OE \) (cmt)

Suy ra: \(KM < KN \) (dây gần tâm hơn thì lớn hơn).

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.2 trên 10 phiếu

Bài tiếp theo

Bài 27 trang 160 SBT toán 9 tập 1
Giải bài 27 trang 160 sách bài tập toán 9. Cho đường tròn (O) và điểm I nằm bên trong đường tròn. Chứng minh rằng dây AB vuông góc với OI tại I ngắn hơn mọi dây khác đi qua I.
Bài 28 trang 160 SBT toán 9 tập 1
Giải bài 28 trang 160 sách bài tập toán 9. Tam giác ABC nội tiếp đường tròn (O) có...
Bài 29 trang 161 SBT toán 9 tập 1
Giải bài 29 trang 161 sách bài tập toán 9. Cho đường tròn (O), hai dây AB, CD bằng nhau và cắt nhau tại điểm I nằm bên trong đường tròn. Chứng minh rằng:...
Bài 30 trang 161 SBT toán 9 tập 1
Giải bài 30 trang 161 sách bài tập toán 9. Cho đường tròn tâm O bán kính 25cm. Hai dây AB, CD song song với nhau và có độ dài theo thứ tự bằng 40cm, 48cm. Tính khoảng cách giữa hai dây ấy.
Bài 31 trang 161 SBT toán 9 tập 1
Giải bài 31 trang 161 sách bài tập toán 9. Cho đường tròn (O), các bán kính OA và OB. Trên cung nhỏ AB lấy các điểm M và N sao cho AM = BN. Gọi C là giao điểm của các đường thẳng AM và BN. Chứng minh rằng:...
Bài 32* trang 161 SBT toán 9 tập 1
Giải bài 32* trang 161 sách bài tập toán 9. Cho đường tròn tâm O bán kính 5dm, điểm M cách O là 3dm...
Bài 33* trang 161 SBT toán 9 tập 1
Giải bài 33* trang 161 sách bài tập toán 9. Cho đường tròn (O), hai dây AB và CD cắt nhau tại điểm M nằm bên trong đường tròn. Gọi H và K theo thứ tự là trung điểm của AB và CD. Cho biết AB >CD, chứng minh rằng MH > MK.
Bài 34* trang 161 SBT toán 9 tập 1
Giải bài 34* trang 161 sách bài tập toán 9. Cho đường tròn (O) và hai điểm A, B nằm bên trong đường tròn và không cùng thuộc một đường kính. Dựng hai dây song song và bằng nhau sao cho điểm A nằm trên một dây, điểm B nằm trên dây còn lại.
Bài 3.1 phần bài tập bổ sung trang 161 SBT toán lớp 9 tập 1
Giải bài 3.1 phần bài tập bổ sung trang 161 sách bài tập toán lớp 9. Cho đường tròn (O) đường kính 6cm, dây AB bằng 2cm. Khoảng cách từ O đến AB bằng:...
Bài 3.2 phần bài tập bổ sung trang 161 SBT toán 9 tập 1
Giải bài 3.2 phần bài tập bổ sung trang 161 sách bài tập toán 9. Cho đường tròn (O), điểm I nằm bên trong đường tròn ( I khác O). Dựng dây AB đi qua I và có độ dài ngắn nhất.
Bài 3.3* phần bài tập bổ sung trang 161 SBT toán 9 tập 1
Giải bài 3.3* phần bài tập bổ sung trang 161 sách bài tập toán 9. Cho đường tròn (O ; 25cm), điểm C cách O là 7cm. Có bao nhiêu dây đi qua C có độ dài là một số nguyên xentimét?
Bài 25 trang 160 SBT toán 9 tập 1
Giải bài 25 trang 160 sách bài tâp toán 9. Cho hình 75, trong đó hai dây CD, EF bằng nhau và vuông góc với nhau tại I, IC = 2cm, ID = 14cm. Tính khoảng cách từ O đến mỗi dây.
Bài 24 trang 160 SBT toán 9 tập 1
Giải bài 24 trang 160 sách bài tập toán 9. Cho hình 74, trong đó MN = PQ. Chứng minh rằng:...