Giải SBT đại số, hình học toán lớp 9 tập 1, tập 2 Bài 3. Liên hệ giữa dây và khoảng cách từ tâm đến dây

Bài 25 trang 160 SBT toán 9 tập 1


Giải bài 25 trang 160 sách bài tâp toán 9. Cho hình 75, trong đó hai dây CD, EF bằng nhau và vuông góc với nhau tại I, IC = 2cm, ID = 14cm. Tính khoảng cách từ O đến mỗi dây.

Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn

Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa - GDCD

Đề bài

Cho hình \(75,\) trong đó hai dây \(CD, EF\) bằng nhau và vuông góc với nhau tại \(I,\) \(IC = 2cm,\) \(ID = 14cm.\) Tính khoảng cách từ \(O\) đến mỗi dây.

Phương pháp giải - Xem chi tiết

Sử dụng kiến thức: Trong một đường tròn: 

+) Hai dây bằng nhau thì cách đều tâm.

+) Đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy. 

Lời giải chi tiết

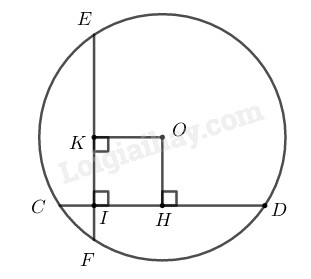
Kẻ \(OH ⊥ CD,\) \(OK ⊥EF\)

Vì tứ giác \(OKIH\) có ba góc vuông nên nó là hình chữ nhật.

Ta có: \(CD = EF\;\; (gt)\)

Suy ra: \(OH = OK\) (hai dây bằng nhau cách đều tâm)

Suy ra tứ giác \(OKIH\) là hình vuông.

Ta có:\(CD = CI + ID = 2 + 14 =16\; (cm)\)

Xét (O) có \(OH ⊥ CD\) mà OH là 1 phần đường kính và CD là dây cung nên \(HC = HD = \displaystyle {{CD} \over 2} = 8\) \((cm)\) (quan hệ giữa đường kính và dây cung)

Suy ra \(IH = HC – CI = 8 – 2 = 6\; (cm)\)

Do đó \(OH = OK =IH= 6\; (cm)\)  (do \(OKIH\) là hình vuông).

Vậy khoảng cách từ \(O\) đến mỗi dây là 6cm.

Loigiaihay.com


Bình chọn:
4.5 trên 15 phiếu
Bài tiếp theo
  • Bài 26 trang 160 SBT toán 9 tập 1

    Giải bài 26 trang 160 sách bài tập toán 9. Cho đường tròn (O), dây AB và dây CD, AB < CD. Giao điểm K của các đường thẳng AB, CD nằm ngoài đường tròn. Đường tròn (O ; OK) cắt KA và KC tại M và N. Chứng minh rằng KM < KN.

  • Bài 27 trang 160 SBT toán 9 tập 1

    Giải bài 27 trang 160 sách bài tập toán 9. Cho đường tròn (O) và điểm I nằm bên trong đường tròn. Chứng minh rằng dây AB vuông góc với OI tại I ngắn hơn mọi dây khác đi qua I.

  • Bài 28 trang 160 SBT toán 9 tập 1

    Giải bài 28 trang 160 sách bài tập toán 9. Tam giác ABC nội tiếp đường tròn (O) có...

  • Bài 29 trang 161 SBT toán 9 tập 1

    Giải bài 29 trang 161 sách bài tập toán 9. Cho đường tròn (O), hai dây AB, CD bằng nhau và cắt nhau tại điểm I nằm bên trong đường tròn. Chứng minh rằng:...

  • Bài 30 trang 161 SBT toán 9 tập 1

    Giải bài 30 trang 161 sách bài tập toán 9. Cho đường tròn tâm O bán kính 25cm. Hai dây AB, CD song song với nhau và có độ dài theo thứ tự bằng 40cm, 48cm. Tính khoảng cách giữa hai dây ấy.

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K9 Ôn Thi Vào Lớp 10 Miễn Phí

>> Học trực tuyến lớp 9 và luyện vào lớp 10 tại Tuyensinh247.com, cam kết giúp học sinh lớp 9 học tốt, hoàn trả học phí nếu học không hiệu quả.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua