Bài 1 trang 5 SBT toán 8 tập 2

Giải bài 1 trang 5 sách bài tập toán 8. Trong các số –2 ; –1,5 ; –1 ; 0,5 ; 2/3 ; 2 ; 3 số nào là nghiệm của mỗi phương trình sau đây .......

Lựa chọn câu để xem lời giải nhanh hơn

Trong các số \(\displaystyle - 2; - 1,5; - 1;0,5;{2 \over 3};2;3\) số nào là nghiệm của mỗi phương trình sau đây :

LG a

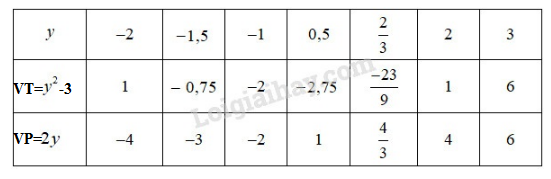
\({y^2} - 3 = 2y\) ;

Phương pháp giải:

Để biết một số có là nghiệm của phương trình hay không ta thay số đó vào hai vế. Nếu hai vế có giá trị bằng nhau thì số đó là nghiệm của phương trình.

Lời giải chi tiết:

\({y^2} - 3 = 2y\)

Vậy phương trình có hai nghiệm : \(y = - 1\) và \(y = 3\).

LG b

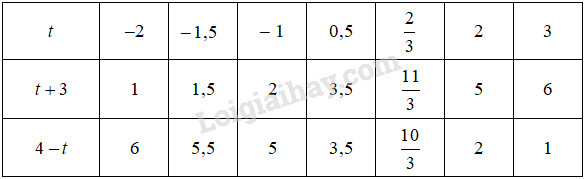
\(t + 3 = 4 - t\) ;

Phương pháp giải:

Để biết một số có là nghiệm của phương trình hay không ta thay số đó vào hai vế. Nếu hai vế có giá trị bằng nhau thì số đó là nghiệm của phương trình.

Lời giải chi tiết:

\(t + 3 = 4 - t\)

Vậy phương trình \(t + 3 = 4 - t\) có một nghiệm : \(t = 0,5\).

LG c

\(\displaystyle{{3x - 4} \over 2} + 1 = 0\).

Phương pháp giải:

Để biết một số có là nghiệm của phương trình hay không ta thay số đó vào hai vế. Nếu hai vế có giá trị bằng nhau thì số đó là nghiệm của phương trình.

Lời giải chi tiết:

\(\displaystyle{{3x - 4} \over 2} + 1 = 0\)

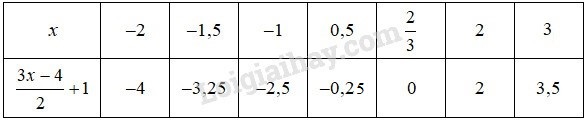
Vậy phương trình \(\displaystyle{{3x - 4} \over 2} + 1 = 0\) có một nghiệm : \(\displaystyle x ={2 \over 3}\).

Bình luận

Chia sẻ

Bình chọn:

4.8 trên 17 phiếu

Bài tiếp theo

Bài 2 trang 5 SBT toán 8 tập 2
Giải bài 2 trang 5 sách bài tập toán 8. Hãy thử lại và cho biết các khẳng định sau có đúng không ......
Bài 3 trang 5 SBT toán 8 tập 2
Giải bài 3 trang 5 sách bài tập toán 8. Cho ba biểu thức 5x – 3 ; x^2 – 3x + 12 và (x + 1)(x – 3). Lập ba phương trình, mỗi phương trình có hai vế là hai trong ba biểu thức đã cho ...
Bài 4 trang 5 SBT toán 8 tập 2
Giải bài 4 trang 5 sách bài tập toán 8. Trong một cửa hàng bán thực phẩm, Tâm thấy cô bán hàng dùng một chiếc cân đĩa. Một bên đĩa cô đặt một quả cân 500g, bên đĩa kia, cô đặt hai gói hàng như nhau và ba quả cân nhỏ, mỗi quả 50g thì cân thăng bằng.
Bài 5 trang 6 SBT toán 8 tập 2
Giải bài 5 trang 6 sách bài tập toán 8. Thử lại rằng phương trình 2mx – 5 = - x + 6m – 2 luôn luôn nhận x = 3 làm nghiệm, dù m lấy bất cứ giá trị nào.
Bài 6 trang 6 SBT toán 8 tập 2
Giải bài 6 trang 6 sách bài tập toán 8.Cho hai phương trình x^2 -5x + 6 = 0; x + (x - 2)(2x + 1) = 2 ...
Bài 7 trang 6 SBT toán 8 tập 2
Giải bài 7 trang 6 sách bài tập toán 8. Tại sao có thể kết luận tập nghiệm của phương trình ....
Bài 8 trang 6 SBT toán 8 tập 2
Giải bài 8 trang 6 sách bài tập toán 8. Chứng minh rằng phương trình x + |x| = 0 nghiệm đúng với mọi x ≤ 0.
Bài 9 trang 6 SBT toán 8 tập 2
Giải bài 9 trang 6 sách bài tập toán 8. Cho phương trình m^2 + 5m + 4)x^2 = m + 4, trong đó m là một số.Chứng minh rằng : a) Khi m = - 4, phương trình nghiệm đúng với mọi giá trị của ẩn....