Giải bài tập Tài liệu Dạy - học Toán lớp 9, Phát triển tư duy đột phá trong dạy học Toán 9 Ôn tập chương 3 - Hình học 9

Bài 9 trang 113 Tài liệu dạy – học Toán 9 tập 2


Giải bài tập Hãy tính diện tích hình vành khăn tạo bởi đường tròn ngoại tiếp và đường tròn nội tiếp tam giác đều ABC cạnh 12 cm.

Đề bài

Hãy tính diện tích hình vành khăn tạo bởi đường tròn ngoại tiếp và đường tròn nội tiếp tam giác đều ABC cạnh 12 cm.

Phương pháp giải - Xem chi tiết

Diện tích hình vành khăn tạo bởi đường tròn ngoại tiếp và đường tròn nội tiếp tam giác đều ABC cạnh 12 cm bằng hiệu diện tích đường tròn ngoại tiếp và đường tròn nội tiếp tam giác đều ABC.

Lời giải chi tiết

 

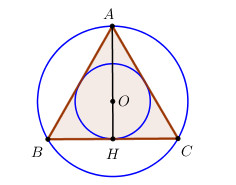
Gọi O là tâm của tam giác đều ABC \( \Rightarrow O\) đồng thời là tâm đường tròn ngoại tiếp và nội tiếp tam giác đều ABC.

Gọi H là trung điểm BC ta có \(AH \bot BC\) (trung tuyến đồng thời là đường cao trong tam giác đều).

\( \Rightarrow \) Bán kính đường tròn ngoại tiếp tam giác ABC là \(R = OA\) và bán kính đường tròn nội tiếp tam giác ABC là \(r = OH\).

Ta có: \(BH = \dfrac{1}{2}BC = 6\,\,\left( {cm} \right)\).

Áp dụng định lí Pytago trong tam giác vuông ABH có:

\(AH = \sqrt {A{B^2} - B{H^2}}  = \sqrt {{{12}^2} - {6^2}} \)\(\, = 6\sqrt 3 \,\,\left( {cm} \right)\).

Vì tam giác ABC đều \( \Rightarrow O\) đồng thời là trọng tâm tam giác ABC

\( \Rightarrow \left\{ \begin{array}{l}R = OA = \dfrac{2}{3}AH = 4\sqrt 3 \,\,\left( {cm} \right)\\r = OH = \dfrac{1}{3}AH = 2\sqrt 3 \,\,\left( {cm} \right)\end{array} \right.\)

\( \Rightarrow \) Diện tích hình tròn ngoại tiếp tam giác ABC là \({S_1} = \pi {R^2} = \pi {\left( {4\sqrt 3 } \right)^2} = 48\pi \,\,\left( {c{m^2}} \right)\)

     Diện tích hình tròn nội tiếp tam giác ABC là \({S_2} = \pi {r^2} = \pi {\left( {2\sqrt 3 } \right)^2} = 12\pi \,\,\left( {c{m^2}} \right)\)

Vậy diện tích hình vành khăn tạo bởi đường tròn ngoại tiếp và đường tròn nội tiếp tam giác đều ABC cạnh 12 cm là \(S = {S_1} - {S_2} = 48\pi  - 12\pi  = 36\pi\)\(\,  \approx 113,04\,\,\left( {c{m^2}} \right)\).

 Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

2K9 Tham Gia Group Giải Đề Thi Vào 10 Các Tỉnh

>> Học trực tuyến lớp 9 & lộ trình Up 10! trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua