Thử tài bạn trang 112 Tài liệu dạy – học Toán 7 tập 2

Giải bài tập Điền vào chỗ trống để hoàn thành phần chứng minh định lí đảo.

Đề bài

Điền vào chỗ trống để hoàn thành phần chứng minh định lí đảo.

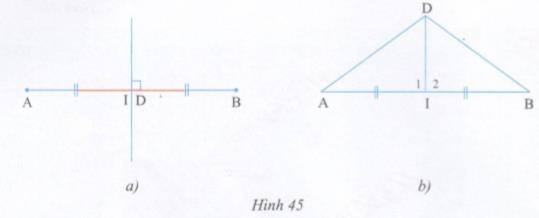
Chứng minh:

Xét hai trường hợp:

* \(D \in AB\) (hình 45a): Vì DA = DB (gt)

Nên D là………….của đoạn thẳng AB, do đó D thuộc…………của đoạn thẳng AB.

* \(D \notin AB\)(hình 45b): Kẻ đoạn thẳng nối D với trung điểm I của đoạn thẳng AB.

Ta có \(\Delta DAI = \Delta DBI\,\,\left( {c.c.c} \right)\)

Suy ra \(\widehat {{I_1}} = ...........\)

Mặt khác: \(\widehat {{I_1}} + \widehat {{I_2}} = {180^o}\,\,\left( {........} \right)\)

Nên ……………..=………….= 90^o

Vậy………..là đường trung trực của đoạn thẳng AB.

Lời giải chi tiết

Chứng minh:

* \(D \in AB\) (hình 45a). Vì DA = DB (gt)

Nên D là trung điểm của đoạn thẳng AB, do đó D thuộc đường trung trực của đoạn thẳng AB.

* \(D \notin AB\) (hình 45b). Kẻ đoạn thẳng nối D với trung điểm của đoạn thẳng AB.

Ta có \(\Delta DAI = \Delta DBI\,\,\left( {c.c.c} \right)\) \( \Rightarrow {\widehat I_1} = {\widehat I_2}.\)

Mặt khác: \({\widehat I_1} + {\widehat I_2} = {180^o}\) (hai góc kề bù). Nên \({\widehat I_1} = {\widehat I_2} = 90^\circ .\)

Vậy DI là đường trung trực của đoạn thẳng AB.

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Hoạt động 14 trang 113 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Dựng đường trung trực của đoạn thẳng AB bằng thước thẳng và compa
Hoạt động 13 trang 111 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Khi làm diều, các nghệ nhân phải chú ý độ cân bằng của cánh diều, khi đó AM = AN, BM = BN (hình 43). Theo em, các điểm A, B có nằm trên đường trung trực của đoạn MN không ?
Thử tài bạn trang 111 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Ở hình 41, biết là đường trung trực của đoạn thẳng AB. Điểm M thuộc đường
Hoạt động 12 trang 110 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Cắt một mảnh giấy trong đó có một mép cắt là đoạn thẳng AB (hình 38a).
Hoạt động 11 trang 109 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Các cột điện trên đường Phạm Văn Đồng TP. Hồ Chí Minh (hình 37). Cho ta hình ảnh đường trung trực của một đoạn thẳng. Điểm A nằm trên đường trung trực của đoạn thẳng BC. Em hãy nhận xét xem điểm A có cách đều hai đầu đoạn thẳng BC không ?