Bài 83* trang 171 SBT toán 9 tập 1

Giải bài 83* trang 171 sách bài tập toán 9. Cho hai đường tròn (O) và (O') cắt nhau tại A và B, OO' = 3cm. Qua A kẻ một đường thẳng cắt các đường tròn (O) và (O') theo thứ tự tại E và F ( A nằm giữa E và F). Tính xem đoạn thẳng EF có độ dài lớn nhất bằng bao nhiêu?

Đề bài

Cho hai đường tròn $(O)$ và $(O')$ cắt nhau tại $A$ và $B,$ $OO' = 3cm.$ Qua $A$ kẻ một đường thẳng cắt các đường tròn $(O)$ và $(O')$ theo thứ tự tại $E$ và $F$ ( $A$ nằm giữa $E$ và $F$ ). Tính xem đoạn thẳng $EF$ có độ dài lớn nhất bằng bao nhiêu $?$

Phương pháp giải - Xem chi tiết

Sử dụng kiến thức:

+) Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.

+) Tứ giác có ba góc vuông là hình chữ nhật.

Lời giải chi tiết

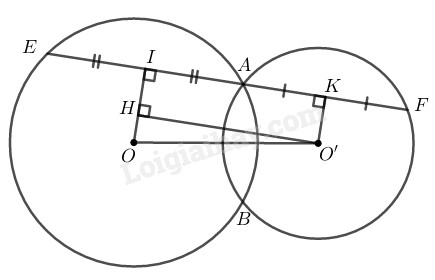
Kẻ $OI ⊥ AE, O'K ⊥ AF$

Trong đường tròn $(O),$ có $OI ⊥ AE$ mà OI là 1 phần đường kính và AE là dây cung nên:

$IA = IE = \displaystyle {1 \over 2}AE$ ( đường kính vuông góc với dây cung)

Trong đường tròn $(O'),$ có $O'K ⊥ AF$ mà O'K là 1 phần đường kính và AF là dây cung nên:

$KA = KF = \displaystyle {1 \over 2}AF$ (đường kính vuông góc với dây cung)

Ta có: $EF = AE + AF$

Suy ra: $EF = 2IA + 2AK$ $= 2(IA + AK) = 2IK \; \;(1)$

Kẻ $O'H ⊥ OI$

Khi đó tứ giác $IHO'K$ là hình chữ nhật ( có ba góc vuông)

Suy ra: $O'H = IK$

Trong tam giác $OHO'$ ta có: $O’H \le {\rm{OO'}}=3\; (cm)$

Suy ra: $IK \le {\rm{OO}}'$ $(2)$

Từ $(1)$ và $(2)$ suy ra: $EF \le {\rm{2OO'}}= 6 (cm)$

Ta có: $EF = 6cm$ khi $H$ và $O$ trùng nhau hay $EF // OO'$

Vậy $EF$ có độ dài lớn nhất bằng $6cm$ khi và chỉ khi $EF // OO'.$

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

3.7 trên 6 phiếu

Bài tiếp theo

Bài 84 trang 171 SBT toán 9 tập 1
Giải bài 84 trang 171 sách bài tập toán 9. Cho tam giác ABC vuông tại A ( AB < AC) nội tiếp đường tròn (O) có đường kính BC. Kẻ dây AD vuông góc với BC. Gọi E là giao điểm của DB và CA. Qua E kẻ đường thẳng vuông góc với BC, cắt BC ở H, cắt AB ở F. Chứng minh rằng:...
Bài 85 trang 172 SBT toán 9 tập 1
Giải bài 85 trang 172 sách bài tập toán 9. Cho đường tròn (O), đường kính AB, điểm M thuộc đường tròn. Vẽ điểm N đối xứng với A qua M. BN cắt đường tròn ở C. Gọi E là giao điểm của AC và BM...
Bài 86 trang 172 SBT toán 9 tập 1
Giải bài 86 trang 172 sách bài tập toán 9. Cho đường tròn (O), đường kính AB, điểm C nằm giữa A và O. Vẽ đường tròn (O) có đường kính CB...
Bài 87 trang 172 SBT toán 9 tập 1
Giải bài 87 trang 172 sách bài tập toán 9. Cho hai đường tròn (O ; R) và (O' ; R') tiếp xúc ngoài tại A ( R > R')...
Bài 88 trang 172 SBT toán 9 tập 1
Giải bài 88 trang 172 sách bài tập toán 9. Cho nửa đường tròn tâm O có đường kính AB. Gọi M là điểm bất kì thuộc nửa đường tròn, H là chân đường vuông góc kẻ từ M đến AB. Vẽ đường tròn (M ; MH). Kẻ các tiếp tuyến AC, BD với đường tròn tâm M ( C và D là các tiếp điểm khác H)...
Bài 2.1 phần bài tập bỏ sung trang 173 SBT toán 9 tập 1
Giải bài 2.1 phần bài tập bỏ sung trang 173 sách bài tập toán 9. Tỉ số bán kính đường tròn nội tiếp và đường tròn ngoại tiếp một tam giác đều bằng:...
Bài 2.2 phần bài tập bổ sung trang 173 SBT toán 9 tập 1
Giải bài 2.2 phần bài tập bổ sung trang 173 sách bài tập toán 9. Cho nửa đường tròn (O) đường kính AB. Trên nửa mặt phẳng bờ AB chứa nửa đường tròn, vẽ các tia tiếp tuyến Ax và By với nửa đường tròn. Gọi M là điểm thuộc nửa đường tròn, D là giao điểm của AM và By, C là giao điểm của BM và Ax, E là trung điểm của BD. Chứng minh rằng:...
Bài 2.3 phần bài tập bổ sung trang 173 SBT toán 9 tập 1
Giải bài 2.3 trang 173 phần bài tập bổ sung sách bài tập toán 9 Tập 1. Cho đường tròn (O) và điểm A cố định trên đường tròn. Gọi xy là tiếp tuyến với đường tròn tại A. Từ một điểm M nằm trên xy, vẽ tiếp tuyến MB với đường tròn. Gọi H là trực tâm của tam giác MAB...
Bài 82 trang 171 SBT toán 9 tập 1
Giải bài 82 trang 171 sách bài tập toán 9. Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài DE, D ∈ (O), E ∈ (O’). Kẻ tiếp tuyến chung tại A, cắt DE ở I. Gọi M là giao điểm của OI và AD, N là giao điểm của O’I và AE...
Bài 81 trang 171 SBT toán 9 tập 1
Giải bài 81 trang 171 sách bài tập toán 9. Cho đoạn thẳng AB, điểm C nằm giữa A và B. Vẽ về một phía của AB các nửa đường tròn có đường kính theo thứ tự là AB, AC, CB. Đường vuông góc với AB tại C cắt nửa đường tròn lớn tại D. DA, DB cắt các nửa đường tròn có đường kính AC, CB theo thứ tự M, N...

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

>> Học trực tuyến Lớp 9 & Lộ trình UP10 trên Tuyensinh247.com

>> Chi tiết khoá học xem: TẠI ĐÂY

Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.