-
PHẦN ĐẠI SỐ - SBT TOÁN 7 TẬP 1
-
CHƯƠNG 1: SỐ HỮU TỈ. SỐ THỰC
- Bài 1. Tập hợp Q các số hữu tỉ
- Bài 2. Cộng, trừ số hữu tỉ
- Bài 3. Nhân, chia số hữu tỉ
- Bài 4. Giá trị tuyệt đối của một số hữu tỉ. Cộng, trừ, nhân, chia số thập phân
- Bài 5. Luỹ thừa của một số hữu tỉ
- Bài 6. Luỹ thừa của một số hữu tỉ (tiếp)
- Bài 7. Tỉ lệ thức
- Bài 8. Tính chất của dãy tỉ số bằng nhau
- Bài 9. Số thập phân hữu hạn. Số thập phân vô hạn tuần hoàn
- Bài 10. Làm tròn số
- Bài 11. Số vô tỉ. Khái niệm về căn bậc hai
- Bài 12. Số thực
- Ôn tập chương 1 - Số hữu tỉ. Số thực
-
CHƯƠNG 2: HÀM SỐ VÀ ĐỒ THỊ
- Bài 1. Đại lượng tỉ lệ thuận
- Bài 2. Một số bài toán về đại lượng tỉ lệ thuận
- Bài 3. Đại lượng tỉ lệ nghịch
- Bài 4. Một số bài toán về đại lượng tỉ lệ nghịch
- Bài 5. Hàm số
- Bài 6. Mặt phẳng toạ độ
- Bài 7. Đồ thị của hàm số y = ax (a khác 0)
- Ôn tập chương 2 - Hàm số và đồ thị
-
-
PHẦN HÌNH HỌC - SBT TOÁN 7 TẬP 1
-
CHƯƠNG 1: ĐƯỜNG THẲNG VUÔNG GÓC. ĐƯỜNG THẲNG SONG SONG
- Bài 1. Hai góc đối đỉnh
- Bài 2. Hai đường thẳng vuông góc
- Bài 3. Các góc tạo bởi một đường thẳng cắt hai đường thẳng
- Bài 4. Hai đường thẳng song song
- Bài 5. Tiên đề Ơ-clit về đường thẳng song song
- Bài 6. Từ vuông góc đến song song
- Bài 7. Định lí
- Ôn tập chương 1 - Đường thẳng vuông góc. Đường thẳng song song
-
CHƯƠNG 2: TAM GIÁC
- Bài 1. Tổng ba góc của một tam giác
- Bài 2. Hai tam giác bằng nhau
- Bài 3. Trường hợp bằng nhau thứ nhất của tam giác cạnh - cạnh - cạnh (c.c.c)
- Bài 4. Trường hợp bằng nhau thứ hai của tam giác cạnh - góc - cạnh (c.g.c)
- Bài 5. Trường hợp bằng nhau thứ ba của tam giác góc - cạnh - góc (g.c.g)
- Bài 6. Tam giác cân
- Bài 7. Định lí Py-ta-go
- Bài 8. Các trường hợp bằng nhau của tam giác vuông
- Bai 9: Thực hành ngoài trời
- Ôn tập chương 2 - Tam giác
-
-
PHẦN ĐẠI SỐ - SBT TOÁN 7 TẬP 2
-
CHƯƠNG 3: THỐNG KÊ
-
CHƯƠNG 4: BIỂU THỨC ĐẠI SỐ
- Bài 1. Khái niệm về biểu thức đại số
- Bài 2. Giá trị của biểu thức đại số
- Bài 3. Đơn thức
- Bài 4. Đơn thức đồng dạng
- Bài 5. Đa thức
- Bài 6. Cộng, trừ đa thức
- Bài 7. Đa thức một biến
- Bài 8. Cộng, trừ đa thức một biến
- Bài 9. Nghiệm của đa thức một biến
- Bài tập ôn chương 4 - Biểu thức đại số
-
-
PHẦN HÌNH HỌC - SBT TOÁN 7 TẬP 2
-
CHƯƠNG 3: QUAN HỆ GIỮA CÁC YẾU TỐ TRONG TAM GIÁC. CÁC ĐƯỜNG ĐỒNG QUY CỦA TAM GIÁC
- Bài 1. Quan hệ giữa góc và cạnh đối diện trong một tam giác
- Bài 2. Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
- Bài 3. Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức tam giác
- Bài 4. Tính chất ba đường trung tuyến của tam giác
- Bài 5. Tính chất tia phân giác của một góc
- Bài 6. Tính chất ba đường phân giác của tam giác
- Bài 7. Tính chất đường trung trực của một đoạn thẳng
- Bài 8. Tính chất ba đường trung trực của tam giác
- Bài 9. Tính chất ba đường cao của tam giác
- Bài tập ôn chương 3 - Quan hệ giữa các yếu tố trong tam giác. Các đường đồng quy trong tam giác
-
ÔN TẬP CUỐI NĂM
-
Bài 8* trang 37 SBT toán 7 tập 2
Giải bài 8* trang 37 sách bài tập toán 7. Cho tam giác ABC có AB < AC. Tia phân giác của góc A cắt BC ở D. So sánh các độ dài BD, DC.
Đề bài
Cho tam giác \(ABC\) có \(AB < AC.\) Tia phân giác của góc \(A\) cắt \(BC\) ở \(D.\) So sánh các độ dài \(BD, DC.\)
Phương pháp giải - Xem chi tiết
Trên cạnh \(AC\) lấy điểm \(E\) sao cho \(AE = AB\)
Sử dụng:
+) Tính chất hai tam giác bằng nhau
+) Trong một tam giác, góc ngoài tại một đỉnh lớn hơn góc trong tại đỉnh không kề với đỉnh đó.
+) Trong một tam giác, đối diện với góc lớn hơn là cạnh lớn hơn.
Lời giải chi tiết
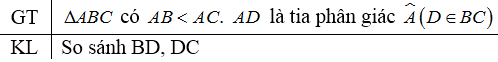
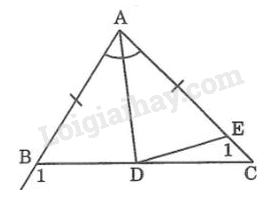
Trên cạnh \(AC\) lấy điểm \(E\) sao cho \(AE = AB\)
Vì \(AB < AC\) nên \(AE < AC\)
Suy ra \(E\) nằm giữa \(A\) và \(C\)
Xét \(∆ABD\) và \(∆AED\) ta có:
+) \(AB = AE\) (theo cách vẽ)
+) \(\widehat {BA{\rm{D}}} = \widehat {E{\rm{AD}}}\) (vì AD là phân giác góc BAC)
+) \(AD\) cạnh chung
Do đó: \(∆ABD = ∆AED\) (c.g.c)
Suy ra \(BD = DE\) (2 cạnh tương ứng)
và \( \widehat {AB{\rm{D}}} = \widehat {A{\rm{ED}}}\) (2 góc tương ứng)
Mà: \(\widehat {AB{\rm{D}}} + \widehat {{B_1}} = 180^\circ \) (2 góc kề bù)
\(\widehat {A{\rm{ED}}} + \widehat {{E_1}} = 180^\circ \) (2 góc kề bù)
Suy ra: \(\widehat {{B_1}} = \widehat {{E_1}}\)
Trong \(∆ABC\) ta có \(\widehat {{B_1}}\) là góc ngoài tại đỉnh \(B.\)
\( \Rightarrow \widehat {{B_1}} > \widehat C\) (góc ngoài tại một đỉnh của tam giác lớn hơn góc trong không kề với đỉnh đó)
Suy ra: \(\widehat {{E_1}} > \widehat C\)
Trong \(∆DEC\) ta có: \(\widehat {{E_1}} > \widehat C\)
\( \Rightarrow DC > DE\) (cạnh đối diện góc lớn hơn là cạnh lớn hơn) mà \(DE=BD\) (chứng minh trên)
Suy ra: \(BD < DC.\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 9* trang 37 SBT toán 7 tập 2
- Bài 10 trang 37 SBT toán 7 tập 2
- Bài 1.1, 1.2, 1.3 phần bài tập bổ sung trang 37 SBT toán 7 tập 2
- Bài 1.4, 1.5, 1.6 phần bài tập bổ sung trang 37, 38 SBT toán 7 tập 2
- Bài 7* trang 37 SBT toán 7 tập 2
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
