Bài 67 trang 167 SBT toán 9 tập 1

Giải bài 67 trang 167 sách bài tập toán 9. Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Kẻ các đường kính AOC, AO’D. Chứng minh rằng ba điểm C, B, D thẳng hàng và AB ⊥ CD.

Đề bài

Cho hai đường tròn \((O)\) và \((O’)\) cắt nhau tại \(A\) và \(B.\) Kẻ các đường kính \(AOC,\) \(AO’D.\) Chứng minh rằng ba điểm \(C, B, D\) thẳng hàng và \(AB ⊥ CD.\)

Phương pháp giải - Xem chi tiết

Sử dụng kiến thức: Để chứng minh ba điểm thẳng hàng ta có thể chứng minh qua ba điểm đó xác định góc bẹt \((\)góc \(180^o)\)

Lời giải chi tiết

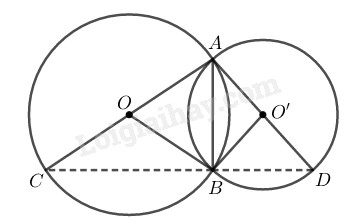
Tam giác \(ABC\) nội tiếp trong đường tròn \((O)\) có \(AC\) là đường kính nên \(\widehat {ABC} = 90^\circ \)

Tam giác \(ABD\) nội tiếp trong đường tròn \((O')\) có \(AD\) là đường kính nên \(\widehat {ABD} = 90^\circ \)

Ta có: \(\widehat {CBD} = \widehat {ABC} + \widehat {ABD}\)\(= 90^\circ + 90^\circ = 180^\circ \)

Vậy ba điểm \(C, B, D\) thẳng hàng và \(AB ⊥ CD\) (vì \(\widehat {ABC} = 90^\circ \)).

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.2 trên 10 phiếu

Bài tiếp theo

Bài 68 trang 168 SBT toán 9 tập 1
Giải bài 68 trang 168 sách bài tập toán 9. Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Gọi I là trung điểm của OO’. Qua A vẽ đường thẳng vuông góc với IA, cắt các đường tròn (O) và (O’) tại C và D (khác A). Chứng minh rằng AC = AD.
Bài 69 trang 168 SBT toán 9 tập 1
Giải bài 69 trang 168 sách bài tập toán 9. Cho hai đường tròn (O) và (O’) cắt nhau tại A và B, trong đó O’ nằm trên đường tròn (O). Kẻ đường kính O’OC của đường tròn (O)...
Bài 70 trang 168 SBT toán 9 tập 1
Giải bài 70 trang 168 sách bài tập toán 9. Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Dây AC của đường tròn (O) tiếp xúc với đường tròn (O’) tại A...
Bài 7.1 phần bài tập bổ sung trang 168 SBT toán 9 tập 1
Giải bài 7.1 phần bài tập bổ sung trang 168 sách bài tập toán 9. Cho h.bs.23, trong đó OA = 3, O'A = 2, AB = 5. Độ dài AC bằng:...
Bài 7.2 phần bài tập bổ sung trang 168 SBT toán 9 tập 1
Giải bài 7.2 phần bài tập bổ sung trang 168 sách bài tập toán 9. Cho hai đường tròn (O) và (O) cắt nhau tại A và B. Một đường thẳng vuông góc với AB tại B cắt các đường tròn (O) và (O) theo thứ tự tại C và D ( khác B)...
Bài 66 trang 167 SBT toán 9 tập 1
Giải bài 66 trang 167 sách bài tập toán 9. Cho hai đường tròn (O), (O’) tiếp xúc nhau tại A như trên hình 78. Chứng minh rằng các bán kính OB và O’C song song với nhau...
Bài 65 trang 167 SBT toán 9 tập 1
Giải bài 65 trang 167 sách bài tập toán 9. Cho hai đường tròn (O) và (O’) cắt nhau tại A và B như trên hình 77...
Bài 64 trang 167 SBT toán 9 tập 1
Giải bài 64 trang 167 sách bài tập toán 9. Cho hình 76, trong đó hai đường tròn (O) và (O’) tiếp xúc nhau tại A. Chứng minh rằng các tiếp tuyến Bx và Cy song song với nhau...