Giải SBT đại số, hình học toán lớp 9 tập 1, tập 2 Bài 8. Đường tròn ngoại tiếp. Đường tròn nội tiếp

Bài 51 trang 108 SBT toán 9 tập 2


Giải bài 51 trang 108 sách bài tập toán 9. Cho ngũ giác đều ABCDE. Gọi I là giao điểm của AD và BE...

Đề bài

Cho ngũ giác đều \(ABCDE.\) Gọi \(I\) là giao điểm của \(AD\) và \(BE.\) Chứng minh \(D{I^2} = AI.AD\)

Phương pháp giải - Xem chi tiết

Ta sử dụng kiến thức:

+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của cung bị chắn.

+) Số đo góc ở tâm chắn mỗi cạnh của đa giác đều \(n\) cạnh bằng \(\dfrac{360^\circ}{n}.\)

+) Nếu \(C\) là một điểm trên cung \(AB\) thì: \(sđ \overparen{AB}=sđ \overparen{AC}+sđ \overparen{CB}.\)

+) Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.

Lời giải chi tiết

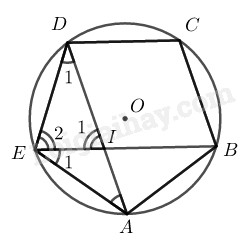
Vẽ đường tròn ngoại tiếp ngũ giác đều \(ABCDE\) 

\(sđ \overparen{AB} = sđ \overparen{BC} = sđ \overparen{CD}\)\(= sđ \overparen{DE} = sđ \overparen{AE}=\dfrac{360^\circ}{5}= 72^\circ\)\(\;\;                (1)\)

\(\widehat {{E_1}} = \displaystyle {1 \over 2} sđ \overparen{AB}\) (tính chất góc nội tiếp)   \(  (2)\)

\(\widehat {{D_1}} =  \displaystyle {1 \over 2} sđ \overparen{AE}\) (tính chất góc nội tiếp)   \(        (3)\)

Từ \((1),\) \((2)\) và \((3)\) suy ra: \(\widehat {{E_1}} = \widehat {{D_1}}\)

Xét \(∆AIE\) và \(∆AED:\)

+) \(\widehat {{E_1}} = \widehat {{D_1}}\) (chứng minh trên)

+) \(\widehat A\) chung

Suy ra: \(∆AIE\) đồng dạng \(∆AED (g.g)\)

Do đó: \( \displaystyle {{AI} \over {AE}} = \displaystyle{{AE} \over {AD}}\)

\( \Rightarrow \) \(AE^2= AI. AD    \)\(\;\; (*)\)

Lại có: \(\widehat {{E_2}} = \displaystyle  {1 \over 2}sđ \overparen{BCD}\) (tính chất góc nội tiếp) hay \(\widehat {{E_2}} =  \displaystyle {1 \over 2} (sđ \overparen{BC} + sđ \overparen{CD}\)) \(\;\;           (4)\)

\(\widehat {{I_1}} =  \displaystyle {1 \over 2} (sđ \overparen{DE} + sđ \overparen{AB}\)) (tính chất góc có đỉnh ở trong đường tròn)  \(                               (5)\)

Từ \((1),\) \((4)\) và \((5)\) suy ra: \(\widehat {{E_2}} = \widehat {{I_1}}\)

\( \Rightarrow \) \(∆DEI\) cân tại \(D\) \( \Rightarrow DE = DI\)

          \(     DE = AE\;\; (gt)\)

Suy ra:\(DI = AE \;\;   (**)\)

Từ \((*)\) và \((**)\) suy ra:\( DI^2= AI. AD\)

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store