-
PHẦN ĐẠI SỐ - SBT TOÁN 9 TẬP 1
-
CHƯƠNG 1: CĂN BẬC HAI. CĂN BẬC BA
- Bài 1. Căn bậc hai
- Bài 2. Căn thức bậc hai và hằng đẳng thức
- Bài 3. Liên hệ giữa phép nhân và phép khai phương
- Bài 4. Liên hệ giữa phép chia và phép khai phương
- Bài 5. Bảng căn bậc hai
- Bài 6. Biến đổi đơn giản biểu thức chứa căn thức bậc hai
- Bài 7. Biến đổi đơn giản biểu thức chứa căn thức bậc hai
- Bài 8. Rút gọn biểu thức chứa căn thức bậc hai
- Bài 9. Căn bậc ba
- Ôn tập chương 1 - Căn bậc hai. Căn bậc ba
-
CHƯƠNG 2: HÀM SỐ BẬC NHẤT
-
-
PHẦN HÌNH HỌC - SBT TOÁN 9 TẬP 1
-
CHƯƠNG 1: HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
-
CHƯƠNG 2: ĐƯỜNG TRÒN
- Bài 1. Sự xác định đường tròn. Tính chất đối xứng của đường tròn
- Bài 2. Đường kính và dây của đường tròn
- Bài 3. Liên hệ giữa dây và khoảng cách từ tâm đến dây
- Bài 4. Vị trí tương đối của đường thẳng và đường tròn
- Bài 5. Dấu hiệu nhận biết tiếp tuyến của đường tròn
- Bài 6. Tính chất của hai tiếp tuyến cắt nhau
- Bài 7. Vị trí tương đối của hai đường tròn
- Bài 8. Vị trí tương đối của hai đường tròn (tiếp theo)
- Ôn tập chương 2 - Đường tròn
-
-
PHẦN ĐẠI SỐ - SBT TOÁN 9 TẬP 2
-
CHƯƠNG 3: HỆ HAI PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
-
CHƯƠNG 4: HÀM SỐ y=ax^2 (a ≠ 0). PHƯƠNG TRÌNH BẬC HAI MỘT ẨN
- Bài 1. Hàm số bậc hai y=ax^2 (a ≠ 0)
- Bài 2. Đồ thị của hàm số bậc hai
- Bài 3. Phương trình bậc hai một ẩn
- Bài 4. Công thức nghiệm của phương trình bậc hai
- Bài 5. Công thức nghiệm thu gọn
- Bài 6. Hệ thức Vi-ét và ứng dụng
- Bài 7. Phương trình quy về phương trình bậc hai
- Bài 8. Giải bài toán bằng cách lập phương trình
- Bài tập ôn chương 4 - Hàm số y=ax^2 (a ≠ 0). Phương trình bậc hai một ẩn
-
-
PHẦN HÌNH HỌC - SBT TOÁN 9 TẬP 2
-
CHƯƠNG 3: GÓC VỚI ĐƯỜNG TRÒN
- Bài 1. Góc ở tâm. Số đo cung
- Bài 2. Liên hệ giữa cung và dây
- Bài 3. Góc nội tiếp
- Bài 4. Góc tạo bởi tia tiếp tuyến và dây cung
- Bài 5. Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh bên ngoài đường tròn
- Bài 6. Cung chứa góc
- Bài 7. Tứ giác nội tiếp
- Bài 8. Đường tròn ngoại tiếp. Đường tròn nội tiếp
- Bài 9. Độ dài đường tròn, cung tròn
- Bài 10. Diện tích hình tròn, hình quạt tròn
- Bài tập ôn chương 3 - Góc với đường tròn
-
CHƯƠNG 4: HÌNH TRỤ - HÌNH NÓN – HÌNH CẦU
-
BÀI TẬP ÔN TẬP CUỐI NĂM
-
Giải SBT đại số, hình học toán lớp 9 tập 1, tập 2
Bài 8. Đường tròn ngoại tiếp. Đường tròn nội tiếp
Bài 45 trang 107 SBT toán 9 tập 2
Giải bài 45 trang 107 sách bài tập toán 9. Vẽ đường tròn tâm O bán kính R = 2 cm rồi vẽ hình tám cạnh đều nội tiếp đường tròn (O; 2 cm). Nêu cách vẽ.
Đề bài
Vẽ đường tròn tâm \(O\) bán kính \(R = 2cm\) rồi vẽ hình tám cạnh đều nội tiếp đường tròn \((O; 2 cm).\) Nêu cách vẽ.
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Tất cả các đỉnh của đa giác đều đều nằm trên một đường tròn. Tất cả các đa giác đều đều có một đường tròn ngoại tiếp.
Lời giải chi tiết
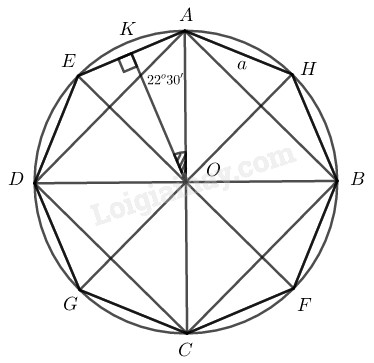
Cách vẽ:
− Vẽ đường tròn \((0; 2 cm)\)
− Vẽ đường kính \(AC ⊥ BD\)
− Nối \(AB, BC, CD, DA\) ta có hình vuông \(ABCD\) nội tiếp đường tròn \((0; 2 cm)\)
− Kẻ đường kính \(EF ⊥ AD;\) đường kính \(GH ⊥ AB\)
Nối \(AE, ED, DG, GC, CF,\)\( FB,\)\( BH,\)\( HA\) ta có đa giác \(AEDGCFBH\) là đa giác đều \(8\) cạnh nội tiếp trong đường tròn \((0; 2cm).\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 46 trang 107 SBT toán 9 tập 2
- Bài 47 trang 108 SBT toán 9 tập 2
- Bài 48 trang 108 SBT toán 9 tập 2
- Bài 49 trang 108 SBT toán 9 tập 2
- Bài 50 trang 108 SBT toán 9 tập 2
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
