 Giải SBT đại số, hình học toán lớp 8 tập 1, tập 2
Giải SBT đại số, hình học toán lớp 8 tập 1, tập 2
 Bài 4. Đường trung bình của tam giác, của hình thang
Bài 4. Đường trung bình của tam giác, của hình thang
Bài 36 trang 84 SBT toán 8 tập 1
Giải bài 36 trang 84 sách bài tập toán 8. Cho tứ giác ABCD. Gọi E, F, I theo thứ tự là trung điểm của AD, BC, AC...
Đề bài
Cho tứ giác \(ABCD.\) Gọi \(E, F, I\) theo thứ tự là trung điểm của \(AD,\) \(BC,\) \(AC.\) Chứng minh rằng:
\(a)\) \(EI// CD,\) \(IF // AB.\)
\(b)\) \(EF \le \displaystyle {{AB + CD} \over 2}\)
Phương pháp giải - Xem chi tiết
\(a)\) Sử dụng định nghĩa, tính chất đường trung bình của tam giác:
+) Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
+) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
\(b)\) Sử dụng bất đẳng thức tam giác: Trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại.
Lời giải chi tiết
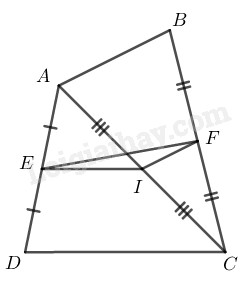
\(a)\) Trong tam giác \(ADC,\) ta có:
\(E\) là trung điểm của \(AD\;\; (gt)\)
\(I\) là trung điểm của \(AC\;\; (gt)\)
Nên \(EI\) là đường trung bình của \(∆ ADC\)
\(⇒ EI // CD\) (tính chất đường trung bình của tam giác) và \(EI =\displaystyle {{CD} \over 2}\)
Trong tam giác \(ABC\) ta có:
\(I\) là trung điểm của \(AC\)
\(F\) là trung điểm của \(BC\)
Nên \(IF\) là đường trung bình của \(∆ ABC\)
\(⇒ IF // AB\) (tính chất đường trung bình của tam giác) và \(IF = \displaystyle {{AB} \over 2}\)
\(b)\) Trong \(∆ EIF\) ta có: \(EF ≤ EI + IF\) (dấu \(“=”\) xảy ra khi \(E, I, F\) thẳng hàng)
Mà \(EI =\displaystyle {{CD} \over 2}{\rm{;}}\,\,IF{\rm{ = }}{{AB} \over 2}\) (chứng minh trên)
\( \Rightarrow {\rm{EF}} \le\displaystyle {{CD} \over 2} + {{AB} \over 2}\)
Vậy \(EF \le \displaystyle {{AB + CD} \over 2}\) (dấu bằng xảy ra khi \(AB // CD\))
Loigiaihay.com












Danh sách bình luận