Giải SBT đại số, hình học toán lớp 9 tập 1, tập 2

Ôn tập chương 2 - Hàm số bậc nhất

Bài 36 trang 70 SBT toán 9 tập 1

Giải bài 36 trang 70 sách bài tập toán 9. Vẽ đồ thị của các hàm số sau trên cùng một mặt phẳng tọa độ:

Đề bài

a) Vẽ đồ thị của các hàm số sau trên cùng một mặt phẳng tọa độ:

\(y = 3x + 6\); (1)

\(y = x + 2\); (2)

\(y = 2x + 4\); (3)

\(y = \dfrac{1}{2}x + 1\). (4)

b) Gọi giao điểm của các đường thẳng (1), (2), (3), (4) với trục hoành là A và với trục tung lần lượt là \({B_1},{B_2},{B_3},{B_4}\) , ta có \(\widehat {{B_1}Ax} = {\alpha _1};\widehat {{B_2}Ax} = {\alpha _2}\); \(\widehat {{B_3}Ax} = {\alpha _3};\widehat {{B_4}Ax} = {\alpha _4}\). Tính các góc \({\alpha _1},{\alpha _2},{\alpha _3},{\alpha _4}\).

( Hướng dẫn : Dùng máy tính bỏ túi CASIO fx – 220 hoặc CASIO fx – 500A hoặc CASIO fx – 500MS … tính \(tg{\alpha _1},tg{\alpha _2},tg{\alpha _3},tg{\alpha _4}\) rồi tính ra các góc tương ứng).

c) Có nhận xét gì về độ dốc của các đường thẳng (1), (2) , (3) , (4)?

Phương pháp giải - Xem chi tiết

Cách vẽ đồ thị hàm số \(y = ax + b\) \((a \ne 0)\)

+ Nếu \(b = 0\) ta có hàm số \(y = ax\) . Đồ thị của \(y = ax\) là đường thẳng đi qua gốc tọa độ \(O(0;0)\) và điểm \(A(1;a)\);

+ Nếu \(b \ne 0\) thì đồ thị \(y = ax + b\) là đường thẳng đi qua các điểm \(A(0;b)\); \(B( - \dfrac{b}{a};0)\).

Đường thẳng \(y = ax + b\) \((a \ne 0)\) có hệ số góc là a và có góc tạo với trục Ox là \(\alpha\) thỏa mãn \(\tan \alpha =a\)

Lời giải chi tiết

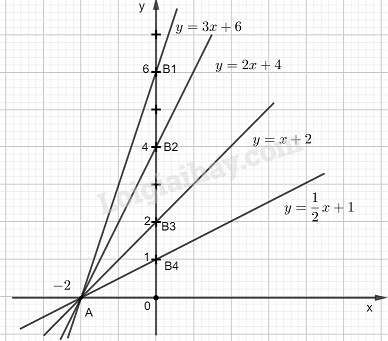
a) *) Vẽ đồ thị của hàm số \(y = 3x + 6\)

Cho \(x = 0\) thì \(y = 6.\) Ta có: \({B_1}\left( {0;6} \right)\)

Cho \(y = 0\) thì \(3x + 6 = 0 \Leftrightarrow x = - 2\). Ta có : \(A(-2 ; 0)\)

Đồ thị của hàm số \(y = 3x + 6\) là đường thẳng \(A{B_1}\)

*) Vẽ đồ thị của hàm số \(y = 2x + 4\)

Cho \(x = 0\) thì \(y = 4.\) Ta có: \({B_2}\left( {0;4} \right)\)

Cho \(y = 0\) thì \(2x + 4 = 0 \Leftrightarrow x = - 2\). Ta có : \(A(-2; 0)\)

Đồ thị của hàm số \(y = 2x + 4\) là đường thẳng \(A{B_2}\) .

*) Vẽ đồ thị của hàm số \(y = x + 2\)

Cho \(x = 0\) thì \(y = 2.\) Ta có: \({B_3}(0;2)\)

Cho \(y = 0\) thì \(x + 2 = 0 \Leftrightarrow x = - 2\). Ta có: \({\rm{A}}\left( { - 2;0} \right)\)

Đồ thị của hàm số \(y = x + 2\) là đường thẳng \(A{B_3}\)

*) Vẽ đồ thị của hàm số \(y = \dfrac{1}{2}x + 1\)

Cho \(x = 0\) thì \(y = 1.\) Ta có: \({B_4}\left( {0;1} \right)\)

Cho \(y = 0\) thì \(\dfrac{1}{2}x + 1 = 0 \Leftrightarrow x = - 2\). Ta có: \({\rm{A}}\left( { - 2;0} \right)\)

Đồ thị của hàm số \(y = \dfrac{1}{2}x + 1\) là đường thẳng \(A{B_4}\)

b) Ta có:

\(\tan{\alpha _1} = 3 \Rightarrow \alpha = {71^0}34'\)

\(\eqalign{
& \tan {\alpha _2} = 2 \Rightarrow {\alpha _2} = {63^0}26' \cr
& \tan {\alpha _3} = 1 \Rightarrow {\alpha _3} = {45^0} \cr
& \tan {\alpha _4} = {1 \over 2} \Rightarrow {\alpha _4} = {26^0}34' \cr} \)

c) Góc tạo bởi các đường thẳng với trục \(Ox\):

\({26^0}34' < {45^0} < {63^0}26' < {71^0}34'\)

Độ dốc của các đường thẳng: \(\left( 1 \right) > \left( 2 \right) > \left( 3 \right) > \left( 4 \right)\).

Rút ra nhận xét:

Với a > 0, khi a càng lớn thì góc tạo bởi đường thẳng \(y = ax + b\) và tia Ox càng lớn, do đó độ dốc của đường thẳng (so với trục nằm ngang Ox) càng lớn.

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.2 trên 5 phiếu

Bài tiếp theo

Bài 37 trang 71 SBT toán 9 tập 1
Giải bài 37 trang 71 sách bài tập toán 9. Cho các điểm M(-1 ; -2) , N(-2; -4), P(2; -3) , Q(3; -4,5). Tìm tọa độ của các điểm M’, N’, P’, Q’ lần lượt đồi xứng với các điểm M,N,P,Q qua trục Ox...
Bài 38 trang 71 SBT toán 9 tập 1
Giải bài 38 trang 71 sách bài tập toán 9. Vẽ đồ thị của các hàm số đã cho trên cùng một mặt phẳng tọa độ...
Bài 35 trang 70 SBT toán 9 tập 1
Bài giải 35 trang 70 sách bài tập toán 9. Tìm các giá trị của m và n trong mỗi trường hợp sau: Đường thẳng (d) đi qua hai điểm ...
Bài 34 trang 70 SBT toán 9 tập 1
Giải bài 34 trang 70 sách bài tập toán 9. Với giá trị nào của m thì đường thẳng (d) đi qua gốc tọa độ ?...
Bài 33 trang 70 SBT toán 9 tập 1
Giải bài 33 trang 70 sách bài tập toán 9. Với điều kiện nào của k và m thì hai đường thẳng sau sẽ trùng nhau ?
Bài 32 trang 70 SBT toán 9 tập 1
Giải bài 32 trang 70 sách bài tập toán 9. Tìm giá trị của a để hai đường thẳng y = (a - 1)x + 2 và y = (3 - a)x +1 song song với nhau.
Bài 31 trang 69 SBT toán 9 tập 1
Giải bài 31 trang 69 sách bài tập toán 9. Với những giá trị nào của m thì đồ thị của các hàm số y = 12x + (5 -m) và y = 3x + (3 + m) cắt nhau tại một điểm trên trục tung ?
Bài 30 trang 69 SBT toán 9 tập 1
Giải bài 30 trang 69 sách bài tập toán 9. Với những giá trị nào của k thì hàm số y = (-k + 9)x + 100 nghịch biến ?