Bài 14 trang 8 SBT toán 9 tập 2

Giải bài 14 trang 8 sách bài tập toán 9. Vẽ hai đường thẳng(d_1):x + y = 2 và(d_2):2x + 3y = 0. Hỏi đường thẳng (d_3):3x + 2y = 10 có đi qua giao điểm của (d_1) và(d_2) hay không?

Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn

Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa - GDCD

Đề bài

Vẽ hai đường thẳng \(\left( {{d_1}} \right):x + y = 2\) và \(\left( {{d_2}} \right):2x + 3y = 0\)

Hỏi đường thẳng \(\left( {{d_3}} \right):3x + 2y = 10\) có đi qua giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) hay không?

Phương pháp giải - Xem chi tiết

Sử dụng:

- Vẽ đường thẳng có phương trình \(ax+by=c,\ (a,b \ne 0)\):

Ta có \(ax+by=c \Leftrightarrow y=-\dfrac{a}{b}x+\dfrac{c}{b}\).

+) Cho \(x=0 \Rightarrow y=\dfrac{c}{b}\) ta được \(A{\left(0; \dfrac{c}{b}\right)}\)

+) Cho \(y=0 \Rightarrow x=\dfrac{c}{a} \) ta được \(B{\left( \dfrac{c}{a}; 0 \right)} \)

Đường thẳng đã cho là đường thẳng đi qua hai điểm \(A,\ B\).

- Hoành độ giao điểm của hai đường thẳng \(y=ax+b\) và \(y=a'x+b'\) là nghiệm của phương trình: \(ax+b=a'x+b'\).

Giải phương trình trên ta tìm được \(x\). Thay giá trị của \(x\) vào phương trình \(y=ax+b\) hoặc \(y=a'x+b'\), ta tìm được tung độ giao điểm.

- Đường thẳng \(ax+by=c\) đi qua điểm \(M(x_0;y_0)\) \( \Leftrightarrow ax_0+by_0=c\).

Lời giải chi tiết

- Vẽ đường thẳng \(\left( {{d_1}} \right):x + y = 2\)

Ta có \(\left( {{d_1}} \right):x + y = 2 \Leftrightarrow y= -x+2\)

Cho \(x = 0 \Rightarrow y = 2\) ta được \(A(0; 2)\)

Cho \(y = 0 \Rightarrow x = 2\) ta được \(B (2; 0)\)

Đường thẳng \(\left( {{d_1}} \right)\) là đường thẳng đi qua hai điểm \(A, \ B\).

- Vẽ đường thẳng \(\left( {{d_2}} \right):2x + 3y = 0\)

Ta có \(\left( {{d_2}} \right):2x + 3y = 0 \Leftrightarrow y = \displaystyle - {2 \over 3}x\)

Cho \(x = 0 \Rightarrow y = 0\) ta được \(O(0; 0)\)

Cho \(x = 3 \Rightarrow y = - 2\) ta được \(C(3; -2)\)

Đường thẳng \(\left( {{d_2}} \right)\) là đường thẳng đi qua hai điểm \(O, \ C\).

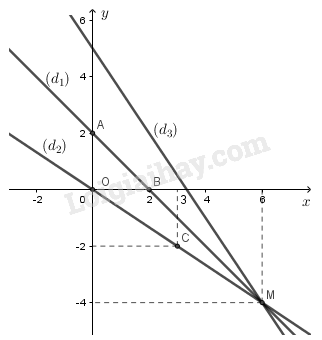
- Hoành độ giao điểm \(M\) của hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) là nghiệm của phương trình:

\(-x+2= \displaystyle - {2 \over 3}x \Leftrightarrow \displaystyle {1 \over 3}x = 2 \\ \Leftrightarrow x = 6\)

Suy ra tung độ giao điểm \(M\) là \( y = -6+2=-4\)

Vậy tọa độ giao điểm của hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) là \( M(6;-4).\)

Thay \(x=6;y=-4\) vào phương trình đường thẳng \(\left( {{d_3}} \right)\) ta được:

\(3.6 + 2.\left( { - 4} \right) =10 \Leftrightarrow 18 - 8 = 10 \\ \Leftrightarrow 10=10 \ \text{(luôn đúng)}.\)

Vậy đường thẳng \(\left( {{d_3}} \right):3x + 2y = 10\) đi qua giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\).

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Bài 15 trang 8 SBT toán 9 tập 2
Giải bài 15 trang 8 sách bài tập toán 9. Hỏi bốn đường thẳng sau có đồng quy không:(d_1):3x+2y=13;(d_2):2x+3y=7; (d_3):x-y=6; (d_4):5x-0y=25?
Bài 2.1, 2.2 phần bài tập bổ sung trang 8 SBT toán 9 tập 2
Giải bài 2.1, 2.2 phần bài tập bổ sung trang 8 sách bài tập toán 9. Không vẽ đồ thị, hãy giải thích vì sao các hệ phương trình sau có nghiệm duy nhất. a)3x=6 và x-3y=2; b) 3x+5y=15 và 2y=-7 ...
Bài 13 trang 8 SBT toán 9 tập 2
Giải bài 13 trang 8 sách bài tập toán 9. Cho hệ phương trình x+0y=-2 và 5x-y=-9. a) Minh họa hình học tập nghiệm của hệ phương trình đã cho. Từ đó xác định nghiệm của hệ; ...
Bài 12 trang 8 SBT toán 9 tập 2
Giải bài 12 trang 8 sách bài tập toán 9. Minh họa hình học tập nghiệm của mỗi hệ phương trình sau: a)2x+3y=7 và x-y=6; b) 3x+2y=13 và 2x-y= -3; c)x+y=1 và 3x+0y=12; ...
Bài 11 trang 7 SBT toán 9 tập 2
Giải bài 11 trang 7 sách bài tập toán 9. Dựa vào vị trí tương đối giữa hai đường thẳng dưới đây, hãy tìm mối liên hệ giữa các hằng số a, b, c và các hằng số a’, b’, c’ để hệ phương trình ...
Bài 10 trang 7 SBT toán 9 tập 2
Giải bài 10 trang 7 sách bài tập toán 9. Cho phương trình 3x – 2y = 5. a) Hãy cho thêm một phương trình bậc nhất hai ẩn để được một hệ có nghiệm duy nhất ...
Bài 9 trang 7 SBT toán 9 tập 2
Giải bài 9 trang 7 sách bài tập toán 9. Hãy biểu diễn y qua x ở mỗi phương trình (nếu có thể ) rồi đoán nhận số nghiệm của mỗi hệ phương trình sau đây và giải thích vì sao (không vẽ đồ thị): a) 4x-9y=3 và -5x-3y=1 ...
Bài 8 trang 6 SBT toán 9 tập 2
Giải bài 8 trang 6 sách bài tập toán 9. Hãy kiểm tra xem mỗi cặp số sau có phải là một nghiệm của hệ phương trình tương ứng hay không: a) (-4;5); 7x-5y=-53 và -2x+9y=53 ...