-
ĐẠI SỐ VÀ GIẢI TÍCH - TOÁN 11
-
HÌNH HỌC - TOÁN 11
-
CHƯƠNG I. PHÉP DỜI HÌNH VÀ PHÉP ĐỒNG DẠNG TRONG MẶT PHẲNG
-
CHƯƠNG II. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG
- Bài 1. Đại cương về đường thẳng và mặt phẳng
- Bài 2. Hai đường thẳng chéo nhau và hai đường thẳng song song
- Bài 3. Đường thẳng và mặt phẳng song song
- Bài 4. Hai mặt phẳng song song
- Bài 5. Phép chiếu song song. Hình biểu diễn của một hình không gian
- Ôn tập chương II - Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
-
CHƯƠNG III. VECTƠ TRONG KHÔNG GIAN. QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN
-
ÔN TẬP CUỐI NĂM HÌNH HỌC - TOÁN 11
-
-
Câu hỏi tự luyện Toán 11
-
TẢI 50 ĐỀ KIỂM TRA 15 PHÚT TOÁN 11
-
TẢI 30 ĐỀ KIỂM TRA 1 TIẾT TOÁN 11
-
TẢI 5 ĐỀ THI GIỮA KÌ 1 TOÁN 11
-
TẢI 25 ĐỀ THI HỌC KÌ 1 TOÁN 11
-
TẢI 6 ĐỀ THI GIỮA HỌC KÌ 2 TOÁN 11
-
TẢI 20 ĐỀ THI HỌC KÌ 2 TOÁN 11
Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học
Bài 4. Hai mặt phẳng vuông góc
Câu hỏi 7 trang 112 SGK Hình học 11
Có tồn tại một hình chóp tứ giác S.ABCD có hai mặt bên (SAB) và (SCD) cùng vuông góc với mặt phẳng đáy hay không ?...
Đề bài
Có tồn tại một hình chóp tứ giác \(S.ABCD\) có hai mặt bên \((SAB)\) và \((SCD)\) cùng vuông góc với mặt phẳng đáy hay không ?
Video hướng dẫn giải
Lời giải chi tiết
Xét trường hợp \(AB\) và \(CD\) cắt nhau tại một điểm \(H\).
Ta lấy \(S\) trên đường thẳng vuông góc với \(mp(ABCD)\) kẻ từ \(H\) thì rõ ràng \((SAB) ⊥(ABCD)\) và \((SCD) ⊥(ABCD)\)
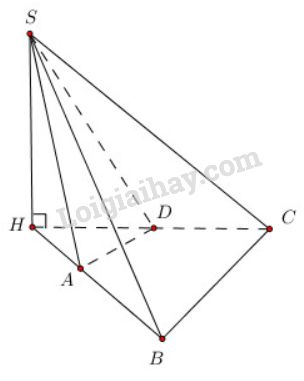
Vậy có tồn tại một hình chóp tứ giác \(S.ABCD\) có hai mặt bên \((SAB)\) và \((SCD)\) cùng vuông góc với mặt phẳng đáy.
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 1 trang 113 SGK Hình học 11
- Bài 2 trang 113 SGK Hình học 11
- Bài 3 trang 113 SGK Hình học 11
- Bài 4 trang 114 SGK Hình học 11
- Bài 5 trang 114 SGK Hình học 11
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
