Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học Bài 4. Hai mặt phẳng vuông góc

Bài 4 trang 114 SGK Hình học 11


Cho hai mặt phẳng

Đề bài

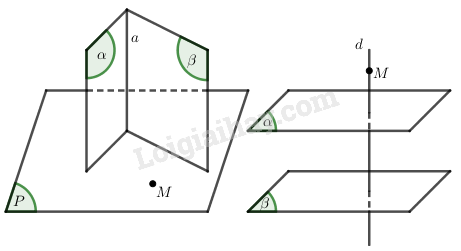
Cho hai mặt phẳng \((\alpha)\), \((\beta)\) cắt nhau và một điểm \(M\) không thuộc \((\alpha)\) và không thuộc \((\beta)\). Chứng minh rằng qua điểm \(M\) có một và chỉ một mặt phẳng \((P)\) vuông góc với \((\alpha)\) và \((\beta)\). Nếu \((\alpha)\) song song với \((\beta)\) thì kết quả trên sẽ thay đổi như thế nào?

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Sử dụng kết quả của định lí: Nếu hai mặt phẳng cắt nhau và cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba đó.

Lời giải chi tiết

Gọi \(a\) là giao tuyến của hai mặt phẳng \((\alpha)\) và \((\beta)\).

Ta có: \(\left\{ \begin{array}{l}\left( P \right) \bot \left( \alpha \right)\\\left( P \right) \bot \left( \beta \right)\\\left( \alpha \right) \cap \left( \beta \right) = a\end{array} \right. \Rightarrow a \bot \left( P \right)\)

Do đó mặt phẳng \((P)\) đi qua \(M\) và vuông góc với đường thẳng \(a\), do đó mặt phẳng \((P)\) là duy nhất.

Nếu  \((\alpha)//(\beta)\) gọi \(d\) là đường thẳng đi qua \(M\) và vuông góc với \((\alpha)\) khi đó ta có \(d\bot (\beta)\).

Như vậy mọi mặt phẳng chứa \(d\) đều vuông góc với  \((\alpha)\) và \((\beta)\).

Do đó khi  \((\alpha)//(\beta)\) thì có vô số mặt phẳng \((P)\) đi qua \(M\) và vuông góc với  \((\alpha)\) và \((\beta)\).

 Loigiaihay.com


Bình chọn:
4.6 trên 26 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho Lớp 11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Hãy viết chi tiết giúp Loigiaihay.com

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Vấn đề em gặp phải là gì ?

Hãy viết chi tiết giúp Loigiaihay.com

Cảm ơn bạn đã sử dụng Loigiaihay.com. Đội ngũ giáo viên cần cải thiện điều gì để bạn cho bài viết này 5* vậy?

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store