-
ĐẠI SỐ VÀ GIẢI TÍCH - TOÁN 11
-
HÌNH HỌC - TOÁN 11
-
CHƯƠNG I. PHÉP DỜI HÌNH VÀ PHÉP ĐỒNG DẠNG TRONG MẶT PHẲNG
-
CHƯƠNG II. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG
- Bài 1. Đại cương về đường thẳng và mặt phẳng
- Bài 2. Hai đường thẳng chéo nhau và hai đường thẳng song song
- Bài 3. Đường thẳng và mặt phẳng song song
- Bài 4. Hai mặt phẳng song song
- Bài 5. Phép chiếu song song. Hình biểu diễn của một hình không gian
- Ôn tập chương II - Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
-
CHƯƠNG III. VECTƠ TRONG KHÔNG GIAN. QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN
-
ÔN TẬP CUỐI NĂM HÌNH HỌC - TOÁN 11
-
-
Câu hỏi tự luyện Toán 11
-
TẢI 50 ĐỀ KIỂM TRA 15 PHÚT TOÁN 11
-
TẢI 30 ĐỀ KIỂM TRA 1 TIẾT TOÁN 11
-
TẢI 5 ĐỀ THI GIỮA KÌ 1 TOÁN 11
-
TẢI 25 ĐỀ THI HỌC KÌ 1 TOÁN 11
-
TẢI 6 ĐỀ THI GIỮA HỌC KÌ 2 TOÁN 11
-
TẢI 20 ĐỀ THI HỌC KÌ 2 TOÁN 11
Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học
Bài 4. Hai mặt phẳng vuông góc
Câu hỏi 1 trang 109 SGK Hình học 11
Cho hai mặt phẳng (α) và (β) vuông góc với nhau và cắt nhau theo giao tuyến d....
Đề bài
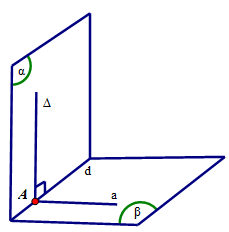
Cho hai mặt phẳng \((α)\) và \((β)\) vuông góc với nhau và cắt nhau theo giao tuyến \(d\). Chứng minh rằng nếu có một đường thẳng \(Δ\) nằm trong \((α)\) và \(Δ\) vuông góc với \(d\) thì \(Δ\) vuông góc với \((β)\)
Video hướng dẫn giải
Lời giải chi tiết
\(Δ\) nằm trong \((α)\) và \(Δ\) vuông góc với \(d ⇒ Δ\) cắt \(d\) tại \(A\)
Từ \(A,\) vẽ đường thẳng \(a\) thuộc \((β)\) và \(a ⊥ d\)
Vì \((α) ⊥ (β)\) nên góc giữa \(Δ\) và \(a\) là \(90^0\) hay \(Δ ⊥ a\)
\(⇒ Δ ⊥ (d,a)\) hay \(Δ ⊥ (β)\)
Loigiaihay.com
Bình luận
Chia sẻ
- Câu hỏi 2 trang 109 SGK Hình học 11
- Câu hỏi 3 trang 109 SGK Hình học 11
- Câu hỏi 4 trang 111 SGK Hình học 11
- Câu hỏi 5 trang 111 SGK Hình học 11
- Câu hỏi 6 trang 112 SGK Hình học 11
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
