-
CHƯƠNG 1: PHÉP NHÂN VÀ PHÉP CHIA ĐA THỨC
-
Chủ đề 1 : Phép nhân đa thức – Hằng đẳng thức đáng nhớ
-
Chủ đề 2 : Phân tích đa thức thành nhân tử
- 1. Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
- 2. Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
- 3. Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
- 4. Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp
- Bài tập - Chủ đề 2 : Phân tích đa thức thành nhân tử
- Luyện tập - Chủ đề 2 : Phân tích đa thức thành nhân tử
-
Chủ đề 3: Phép chia đa thức
-
Ôn tập chương 1 - Phép nhân và phép chia đa thức
-
-
CHƯƠNG 2: PHÂN THỨC ĐẠI SỐ
-
CHƯƠNG 1. TỨ GIÁC
-
Chủ đề 1 : Tứ giác – Hình thang
-
Chủ đề 2 : Hình bình hành – Hình chữ nhật – Hình thoi – Hình vuông
- 1. Đối xứng trục
- 2. Hình bình hành
- 3. Đối xứng tâm
- 4. Hình chữ nhật
- 5. Tập hợp các điểm cách đều một đường thẳng cho trước
- 6. Hình thoi
- 7. Hình vuông
- Bài tập - Chủ đề 2 : Hình bình hành – Hình chữ nhật – Hình thoi – Hình vuông
- Luyện tập - Chủ đề 2 : Hình bình hành – Hình chữ nhật – Hình thoi – Hình vuông
-
Ôn tập chương 1 - Tứ giác
-
-
CHƯƠNG 2. ĐA GIÁC. DIỆN TÍCH ĐA GIÁC
-
CHƯƠNG 3 : PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN – GIẢI BÀI TOÁN BẰNG CÁCH LẬP PHƯƠNG TRÌNH
-
CHƯƠNG 4. BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
-
CHƯƠNG 3. TAM GIÁC ĐỒNG DẠNG
-
Chủ đề 1 : Định lí Thales
-
Chủ đề 2 : Tam giác đồng dạng và ứng dụng
- 1. Khái niệm hai tam giác đồng dạng
- 2. Trường hợp đồng dạng thứ nhất (c.c.c)
- 3. Trường hợp đồng dạng thứ hai (c.g.c)
- 4. Trường hợp đồng dạng thứ ba (g.g)
- 5. Các trường hợp đồng dạng của tam giác vuông
- 6. Ứng dụng thực tế của tam giác đồng dạng
- Bài tập - Chủ đề 2 : Tam giác đồng dạng và ứng dụng
- Luyện tập - Chủ đề 2 : Tam giác đồng dạng và ứng dụng
-
-
CHƯƠNG 4 : HÌNH LĂNG TRỤ ĐỨNG – HÌNH CHÓP ĐỀU
-
ÔN TẬP CUỐI NĂM - TÀI LIỆU DẠY-HỌC TOÁN 8
Giải bài tập Tài liệu Dạy - học Toán lớp 8, Phát triển tư duy đột phá trong dạy học Toán 8
Luyện tập - Chủ đề 1 : Định lí Thales
Bài tập 18 trang 71 Tài liệu dạy – học Toán 8 tập 2
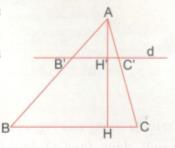
Giải bài tập Tam giác ABC có đường cao AH. Đường thẳng d // BC cắt các cạnh AB, AC và đường cao AH theo thứ tự tại các điểm B’, C’ và H’ (xem hình vẽ).
Đề bài
Tam giác ABC có đường cao AH. Đường thẳng d // BC cắt các cạnh AB, AC và đường cao AH theo thứ tự tại các điểm B’, C’ và H’ (xem hình vẽ).
a) Chứng minh rằng: \({{AH'} \over {AH}} = {{B'C'} \over {BC}}\)
b) Áp dụng: Cho biết \(AH' = {1 \over 3}AH\) và diện tích tam giác ABC là 67,5 cm2. Tính diện tích tam giác AB’C’.
Lời giải chi tiết
a) ∆ABC có \(H'C'//HC\) \((d//BC,H',C' \in d,H \in BC)\)
\( \Rightarrow {{AH'} \over {AH}} = {{AC'} \over {AC}}\) (định lý Thales) (1)
∆ABC có \(B'C'//BC(d//BC;B',C' \in d)\)
\( \Rightarrow {{AC'} \over {AC}} = {{B'C'} \over {BC}}\) (hệ quả của định lý Thales) (2)
Từ (1) và (2) suy ra \({{AH'} \over {AH}} = {{B'C'} \over {BC}}\)
b) Ta có
\(\left\{ \matrix{ AH \bot BC(AH\,là\,đường\,cao) \hfill \cr B'C'//BC \hfill \cr} \right.\)\(\, \Rightarrow AH \bot B'C' \)
\(\Rightarrow AH' \bot B'C'(H' \in AH)\)
Vì \(AH' = {1 \over 3}AH \Rightarrow {{AH'} \over {AH}} = {1 \over 3} \)
\(\Rightarrow {{B'C'} \over {BC}} = {{AH'} \over {AH}} = {1 \over 3}\)
Ta có: \({{{S_{AB'C'}}} \over {{S_{ABC}}}} = {{{1 \over 2}AH'.B'C'} \over {{1 \over 2}AH.BC}} = {{AH'} \over {AH}}.{{B'C'} \over {BC}} \)\(\,= {1 \over 3}.{1 \over 3} = {1 \over 9}\)
\(\Rightarrow {{{S_{AB'C'}}} \over {67,5}} = {1 \over 9}\)
Do đó \({S_{AB'C'}} = {{67,5} \over 9} = 7,5(c{m^2})\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài tập 19 trang 71 Tài liệu dạy – học Toán 8 tập 2
- Bài tập 20 trang 71 Tài liệu dạy – học Toán 8 tập 2
- Bài tập 17 trang 71 Tài liệu dạy – học Toán 8 tập 2
- Bài tập 16 trang 70 Tài liệu dạy – học Toán 8 tập 2
- Bài tập 15 trang 70 Tài liệu dạy – học Toán 8 tập 2
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay
Tham Gia Group Dành Cho 2K10 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến lớp 9 & lộ trình Up 10! trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3 bước: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.
 |
 |
 |
 |
 |
 |
