Giải SBT toán hình học và giải tích 12 nâng cao Bài 3. Phương trình đường thẳng - SBT Toán 12 Nâng cao

Bài 79 trang 135 Sách bài tập Hình học lớp 12 Nâng cao


Cho hình chóp S.ABCD

Lựa chọn câu để xem lời giải nhanh hơn

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng (ABCD) và SA=2a. Gọi M, N lần lượt là trung điểm của các cạnh SA, SD.

LG a

Tính khoảng cách từ đỉnh A tới mặt phẳng (BCM) và khoảng cách giữa hai đường thẳng SB, CN.

Lời giải chi tiết:

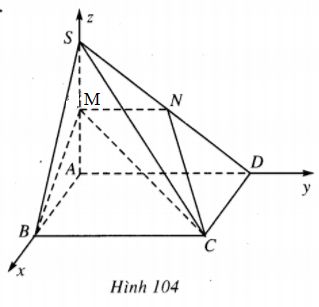
 Chọn hệ trục Oxyz sao cho gốc O là điểm A, tia Ox chứa AB, tia Oy chứa AD và tia Oz chứa SA (h. 104).

Khi đó

\(\eqalign{  & A = \left( {0;0;0} \right),B = \left( {a;0;0} \right),  \cr  & C = \left( {a;a;0} \right),D = \left( {0;a;0} \right),  \cr  & S = \left( {0;0;2a} \right),M\left( {0;0;a} \right),  \cr  & N = \left( {0;{a \over 2};a} \right). \cr} \)

\(\overrightarrow {BC}  = \left( {0;a;0} \right),\)

\(\overrightarrow {BM}  = \left( { - a;0;a} \right)\)

\( \Rightarrow \left[ {\overrightarrow {BC} ,\overrightarrow {BM} } \right] = \left( {\left| {\matrix{   a & 0  \cr   0 & a  \cr  } } \right|;\left| {\matrix{   0 & 0  \cr   a & { - a}  \cr  } } \right|;\left| {\matrix{   0 & a  \cr   { - a} & 0  \cr  } } \right|} \right)\)

                             \(= \left( {{a^2};0;{a^2}} \right).\)

Do đó, mặt phẳng (BCM) có vectơ pháp tuyến là (1; 0; 1), suy ra phương trình mặt phẳng (BCM) là:

\(1\left( {x - a} \right) + 1\left( {z - 0} \right) = 0 \Leftrightarrow x + z -a= 0.\)

Vậy khoảng cách từ A đến mp(BCM)

        \(d\left( {A,\left( {BCM} \right)} \right) = {{\left| { - a} \right|} \over {\sqrt {{1^2} + {1^2}} }} = {a \over {\sqrt 2 }}.\)

Ta lại có: \(\overrightarrow {BS}  = \left( { - a;0;2a} \right),\overrightarrow {CN}  = \left( { - a; - {a \over 2};a} \right),\)

\(\overrightarrow {SC}  = \left( {a;a; - 2a} \right).\)

Suy ra

\(\left[ {\overrightarrow {BS} ,\overrightarrow {CN} } \right] \)

\(= \left( {\left| {\matrix{   0 & {2a}  \cr   { - {a \over 2}} & a  \cr  } } \right|;\left| {\matrix{   {2a} & { - a}  \cr   a & { - a}  \cr  } } \right|;\left| {\matrix{   { - a} & 0  \cr   { - a} & { - {a \over 2}}  \cr  } } \right|} \right) \)

\(= \left( {{a^2}; - {a^2};{{{a^2}} \over 2}} \right)\)

\( \Rightarrow \left[ {\overrightarrow {BS} ,\overrightarrow {CN} } \right].\overrightarrow {SC}  = {a^3} - {a^3} - {a^3} =  - {a^3}.\)

Vậy khoảng cách giữa hai đường thẳng SB và CN là

\(d\left( {SB,CN} \right) = {{\left| {\left[ {\overrightarrow {BS} ,\overrightarrow {CN} } \right].\overrightarrow {CN} } \right|} \over {\left| {\left[ {\overrightarrow {BS} ,\overrightarrow {CN} } \right]} \right|}} \)

                       \(= {{\left| { - {a^3}} \right|} \over {\sqrt {{a^4} + {a^4} + {{{a^4}} \over 4}} }} = {{{a^3}} \over {{{3{a^2}} \over 2}}} = {{2a} \over 3}.\)

LG b

Tính cosin của góc giữa hai mặt phẳng (SCD) và (SBC).

Lời giải chi tiết:

Vì \(\left[ {\overrightarrow {SC} ,\overrightarrow {SD} } \right] = \left( {0;2{a^2};{a^2}} \right)\) nên mp(SCD) có vectơ pháp tuyến \(\overrightarrow n  = \left( {0;2;1} \right).\)

Vì \(\left[ {\overrightarrow {SB} ,\overrightarrow {SC} } \right] = \left( {2{a^2};0;{a^2}} \right)\) nên mp(SBC) có vectơ pháp tuyến \(\overrightarrow {n'}  = \left( {2;0;1} \right).\)

Gọi \(\varphi \) là góc giữa hai mặt phẳng (SCD) và (SBC), ta có

        \(\cos \varphi  = {{\left| {\overrightarrow n .\overrightarrow {n'} } \right|} \over {\left| {\overrightarrow n } \right|\left| {\overrightarrow {n'} } \right|}} = {{\left| { - 1} \right|} \over {\sqrt 5 .\sqrt 5 }} = {1 \over 5}.\)

LG c

Tính tỉ số thể tích giữa hai phần của hình chóp S.ABCD chia bởi mặt phẳng (BCM).

Lời giải chi tiết:

\({V_{S.ABCD}} = {1 \over 3}{a^2}.2a = {2 \over 3}{a^3}.\)

Vì M là trung điểm của SA suy ra \(d\left( {S,\left( {BCM} \right)} \right) = d\left( {A,\left( {BCM} \right)} \right) = {a \over {\sqrt 2 }}.\)

Hình chóp S.ABCD bị mp(BCM) chia làm 2 phần, trong đó có một phần là hình chóp S.BCNM. Hình chóp này có đường cao bằng \(d\left( {S,\left( {BCM} \right)} \right) = {a \over {\sqrt 2 }}\) và đáy là hình thang BCNM có diện tích bằng \({1 \over 2}\left( {a + {a \over 2}} \right)a\sqrt 2  = {{3\sqrt 2 {a^2}} \over 4}.\)

Suy ra: \({V_{S.BCNM}} = {1 \over 3}.{{3\sqrt 2 {a^2}} \over 4}.{a \over {\sqrt 2 }} = {{{a^3}} \over 4}.\)

Vậy tỉ số thể tích giữa hai phần của hình chóp S.ABCD chia bởi mp(BCM) là: \({{{{{a^3}} \over 4}} \over {{{2{a^3}} \over 3} - {{{a^3}} \over 4}}} = {3 \over 5}.\)

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay

Báo lỗi - Góp ý

>> Luyện thi TN THPT & ĐH năm 2024 trên trang trực tuyến Tuyensinh247.com. Học mọi lúc, mọi nơi với Thầy Cô giáo giỏi, đầy đủ các khoá: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng; Tổng ôn chọn lọc.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua