Giải SBT toán hình học và giải tích 12 nâng cao Bài 3. Phương trình đường thẳng - SBT Toán 12 Nâng cao

Bài 77 trang 135 Sách bài tập Hình học lớp 12 Nâng cao


Viết phương trình đường vuông góc chung của các cặp đường thẳng sau :

Lựa chọn câu để xem lời giải nhanh hơn

Viết phương trình đường vuông góc chung của các cặp đường thẳng sau :

LG a

\(\eqalign{  & \;\;d:{{x - 2} \over 2} = {{y - 3} \over 3} = {{z + 4} \over { - 5}},\cr&\;\;\;\;\;d':{{x + 1} \over 3} = {{y - 4} \over { - 2}} = {{z - 4} \over { - 1}}\cr} \)

Lời giải chi tiết:

Cách 1: Ta có \(\overrightarrow {{u_d}}  = \left( {2;3; - 5} \right),\overrightarrow {{u_{d'}}}  = \left( {3; - 2; - 1} \right).\)

Khi đó vì \(\left[ {\overrightarrow {{u_d}} ,\overrightarrow {{u_{d'}}} } \right] = \left( { - 13; - 13; - 13} \right)\) nên đường vuông góc chung \(\Delta \) có một vectơ chỉ phương là \(\overrightarrow u  = \left( {1;1;1} \right).\)

Gọi \(\left( \alpha  \right)\) là mặt phẳng chứa d và \(\Delta \) thì \(\left( \alpha  \right)\) đi qua \({M_o}(2;3; - 4)\) và có vectơ pháp tuyến \(\overrightarrow {{n_\alpha }}  = \left[ {\overrightarrow {{u_d}} ,\overrightarrow u } \right] = \left( {8, - 7, - 1} \right).\)

Có phương trình của mp\(\left( \alpha  \right)\) là: \(8\left( {x - 2} \right) - 7\left( {y - 3} \right) - 1\left( {z + 4} \right) = 0\)

\( \Leftrightarrow 8x - 7y - z + 1 = 0.\)

Gọi \(\left( \beta  \right)\) là mặt phẳng chứa \(d'\) và \(\Delta \) thì \(\left( \beta  \right)\)  đi qua điểm \(M_o'\left( { - 1;4;4} \right)\) và có vectơ pháp tuyến \(\overrightarrow {{n_\beta }}  = \left[ {\overrightarrow u ,\overrightarrow {{u_{d'}}} } \right] = \left( {1;4; - 5} \right).\)

Phương trình của mp\(\left( \beta  \right)\) là :\(1\left( {x + 1} \right) + 4\left( {y - 4} \right) - 5\left( {z - 4} \right) = 0\)

\( \Leftrightarrow x + 4y - 5z + 5 = 0.\)

Vậy đường vuông góc chung \(\Delta \) của \(d\) và \(d'\) là giao tuyến của hai mặt phẳng \(\left( \alpha  \right)\) và \(\left( \beta  \right)\) . Nó có phương trình tham số là:

                               \(\left\{ \matrix{  x = t \hfill \cr  y = t \hfill \cr  z = 1 + t. \hfill \cr}  \right.\)

Cách 2: Điểm \(M \in d\) có toa độ là \(M = \left( {2 + 2t;3 + 3t; - 4 - 5t} \right).\)

Điểm \(N \in d'\) có toa độ là \(N = \left( { - 1 + 3t';4 - 2t';4 - t'} \right)\)

\( \Rightarrow \overrightarrow {MN}  = \left( { - 3 + 3t' - 2t;1 - 2t' - 3t;8 - t' + 5t} \right).\)

MN là đường vuông góc chung của \(d\) và \(d'\) khi và chỉ khi

 \(\left\{ \matrix{  \overrightarrow {MN} .\overrightarrow {{u_d}}  = 0 \hfill \cr  \overrightarrow {MN} .\overrightarrow {{u_{d'}}}  = 0 \hfill \cr}  \right.\)

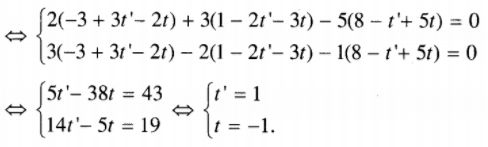
Suy ra \(M = \left( {0;0;1} \right),N = \left( {2;2;3} \right) \Rightarrow \overrightarrow {MN}  = \left( {2;2;2} \right).\)

Vậy phương trình chính tắc của đường vuông góc chung \(\Delta \) là

\({x \over 1} = {y \over 1} = {{z - 1} \over 1}.\)

LG b

\(\eqalign{  & \;\;d:\left\{ \matrix{  x = 2 + t \hfill \cr  y = 1 - t \hfill \cr  z = 2t \hfill \cr}  \right.,d':\left\{ \matrix{  x = 2 - 2t'. \hfill \cr  y = 3 \hfill \cr  z = t'. \hfill \cr}  \right. \cr} \)

Lời giải chi tiết:

\({{x - 2} \over 1} = {{y - 3} \over 5} = {z \over 2}.\)

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay

Báo lỗi - Góp ý

>> Luyện thi TN THPT & ĐH năm 2024 trên trang trực tuyến Tuyensinh247.com. Học mọi lúc, mọi nơi với Thầy Cô giáo giỏi, đầy đủ các khoá: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng; Tổng ôn chọn lọc.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua