Giải SBT toán hình học và giải tích 12 nâng cao Bài 3. Phương trình đường thẳng - SBT Toán 12 Nâng cao

Bài 74 trang 134 Sách bài tập Hình học lớp 12 Nâng cao


a)Cho hai điểm A(3;1;0), B(-9;4;9)

Lựa chọn câu để xem lời giải nhanh hơn

LG a

Cho hai điểm A(3;1;0), B(-9;4;9) và \(mp\left( \alpha  \right):2x - y + z + 1 = 0.\) Tìm tọa độ điểm M trên \(\left( \alpha  \right)\) sao cho \(\left| {MA - MB} \right|\) đạt giá trị lớn nhất.

Lời giải chi tiết:

\(\eqalign{

& P(A) = 2.3 - 1 + 0 + 1 = 6 \cr 
& P(B) = 2.( - 9) - 4 + 9 + 1 = - 12 \cr 
& P(A).P(B) = 6.\left( { - 12} \right) < 0 \cr} \)

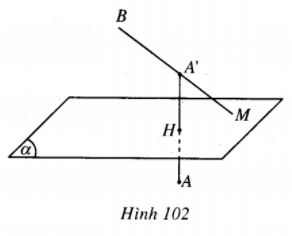
Do đó hai điểm A, B nằm khác phía đối với mặt phẳng \((\alpha )\).

Gọi A' là điểm đối xứng của điểm A qua mặt phẳng (\(\alpha \)), ta có :

\(\left| {MA - MB} \right| = \left| {MA' - MB} \right| \le A'B\)  (không đổi).

Dấu "=" xảy ra khi A' nằm giữa hai điểm B, M hay M là giao điểm của đường thẳng A'B với mp(\(\alpha \)).

Vậy bài toán được giải theo trình tự sau

* Xác định điểm A' đối xứng với điểm A qua mp(\(\alpha \)),

 Ta tìm được A' = (-1 ; 3 ; -2).

* Tìm giao điểm M của đường thẳng A'B với mp(\(\alpha \)).

Đường thẳng A'B có phương trình: \(\left\{ \matrix{  x =  - 1 + 8t \hfill \cr  y = 3 - t \hfill \cr  z =  - 2 - 11t. \hfill \cr}  \right.\)

Toạ độ điểm M(x; y; z) thoả mãn hệ:

            \(\left\{ \matrix{  x =  - 1 + 8t \hfill \cr  y = 3 - t \hfill \cr  z =  - 2 - 11t \hfill \cr  2x - y + z + 1 = 0 \hfill \cr}  \right. \Rightarrow t = 1 \Rightarrow M = (7;2; - 13).\)

Vậy \(\left| {MA - MB} \right|\) lớn nhất khi \(M = (7;2; - 13).\)

LG b

Cho hai điểm A(3;1;1), B(7;3;9) và \(mp\left( \alpha  \right):x + y + z + 3 = 0.\) Tìm điểm M trên \(\left( \alpha  \right)\) để \(\left| {\overrightarrow {MA}  + \overrightarrow {MB} } \right|\) đạt giá trị nhỏ nhất.

Lời giải chi tiết:

Gọi I là trung điểm của đoạn \(AB \Rightarrow I = (5;2;5).\)

Ta có \(\overrightarrow {MA}  + \overrightarrow {MB}  = 2\overrightarrow {MI}  \Rightarrow \left| {\overrightarrow {MA}  + \overrightarrow {MB} } \right| = 2MI.\)

Vậy \(\left| {\overrightarrow {MA}  + \overrightarrow {MB} } \right|\) nhỏ nhất \( \Leftrightarrow \) MI nhỏ nhất với I cố định và \(M \in (\alpha ) \Leftrightarrow M\) là hình chiếu vuông góc với I trên mp(\(\alpha \)).

Toa độ của \(M(x;y;z)\) là nghiệm của hệ:

                    \(\left\{ \matrix{  x = 5 + t \hfill \cr  y = 2 + t \hfill \cr  z = 5 + t \hfill \cr  x + y + z + 3 = 0 \hfill \cr}  \right. \Rightarrow t =  - 5 \Rightarrow M = (0; - 3;0).\)

Kết luận: \(\left| {\overrightarrow {MA}  + \overrightarrow {MB} } \right|\) nhỏ nhất \( { = 2MI = 10\sqrt 3 } \) khi M= (0; -3; 0).

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay

Báo lỗi - Góp ý

Group Ôn Thi ĐGNL & ĐGTD Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store