Bài 2 trang 16 Tài liệu dạy – học Toán 9 tập 2

Giải bài tập Hãy viết phương trình tổng quát và biểu diễn tập nghiệm trong mặt phẳng Oxy của các phương trình sau:

Đề bài

Hãy viết phương trình tổng quát và biểu diễn tập nghiệm trong mặt phẳng Oxy của các phương trình sau:

\(\begin{array}{l}a)\,\,3x - y = 2\\b)\,\,2x - 3y = 6\\c)\,\,0x + 2y = - 2\\d)\,\,3x - 0y = 6\end{array}\)

Phương pháp giải - Xem chi tiết

Đường thẳng \(ax + by = c \Leftrightarrow by = - ax + c\)\(\, \Leftrightarrow y = - \dfrac{a}{b}x + \dfrac{c}{b}\)

Do đó phương trình \(ax + by = c\) có nghiệm tổng quát là \(\left( {x; - \dfrac{a}{b}x + \dfrac{c}{b}} \right)\) với \(x \in R\) và tập nghiệm được biểu diễn trên mặt phẳng tọa độ Oxy bởi đường thẳng \(y = - \dfrac{a}{b}x + \dfrac{c}{b}\,\,\left( d \right)\)

Lời giải chi tiết

a) Ta có: \(3x - y = 2 \Leftrightarrow y = 3x - 2\).

Do đó phương trình \(3x - y = 2\) có nghiệm tổng quát là \(\left( {x;3x - 2} \right)\) với \(x \in R\) và tập nghiệm được biểu diễn trên mặt phẳng tọa độ Oxy bởi đường thẳng \(y = 3x - 2\,\,\left( d \right)\).

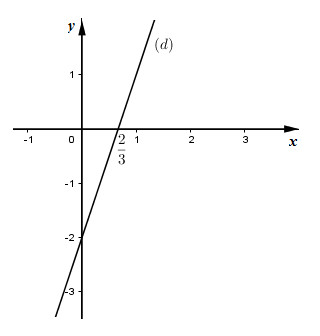
b) Ta có: \(2x - 3y = 6 \)

\(\Leftrightarrow 3y = 2x - 6 \Leftrightarrow y = \dfrac{2}{3}x - 2\)

Do đó phương trình \(2x - 3y = 6\) có nghiệm tổng quát là \(\left( {x;\dfrac{2}{3}x - 2} \right)\) với \(x \in R\) và tập nghiệm được biểu diễn trên mặt phẳng tọa độ Oxy bởi đường thẳng \(y = \dfrac{2}{3}x - 2\,\,\left( d \right)\).

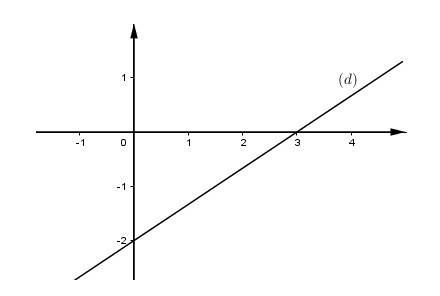
c) \(0x + 2y = - 2 \Leftrightarrow y = - 1\)

Do đó phương trình \(0x + 2y = - 2\) có nghiệm tổng quát là \(\left( {x; - 1} \right)\) với \(x \in R\) và tập nghiệm được biểu diễn trên mặt phẳng tọa độ Oxy bởi đường thẳng \(y = - 1\,\,\left( d \right)\)

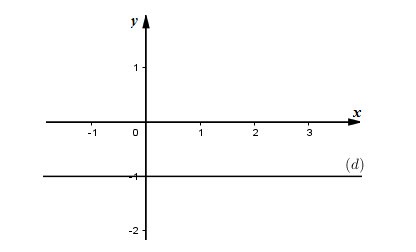
d) \(3x - 0y = 6 \Leftrightarrow 3x = 6 \Leftrightarrow x = 2\).

Do đó phương trình \(3x + 0y = 6\) có nghiệm tổng quát là \(\left( {2;y} \right)\) với \(y \in R\) và tập nghiệm được biểu diễn trên mặt phẳng tọa độ Oxy bởi đường thẳng \(x = 2\,\,\left( d \right)\)

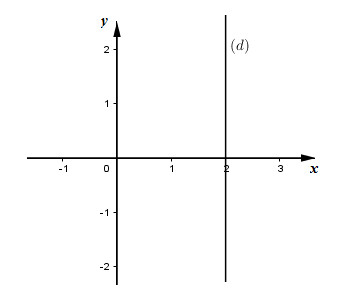
Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Bài 3 trang 16 Tài liệu dạy – học Toán 9 tập 2
Giải bài tập Bạn Lan chuẩn bị bữa điểm tâm gồm đậu phộng với mì xào. Biết rằng cứ mỗi 30 g đậu phộng
Bài 4 trang 16 Tài liệu dạy – học Toán 9 tập 2
Giải bài tập Tìm số nghiệm của các hệ phương trình sau:
Bài 5 trang 16 Tài liệu dạy – học Toán 9 tập 2
Giải bài tập Xét sự tương đương của các cặp hệ phương trình sau:
Bài 6 trang 16 Tài liệu dạy – học Toán 9 tập 2
Giải bài tập Cho hệ phương trình
Bài 7 trang 16 Tài liệu dạy – học Toán 9 tập 2
Giải bài tập Nếu ta biết được hai nghiệm phân biệt của một hệ phương trình bậc nhất hai ẩn thì hệ phương trình có bao nhiêu nghiệm ?
Bài 1 trang 16 Tài liệu dạy – học Toán 9 tập 2
Giải bài tập Cho phương trình bậc nhất