Giải bài tập Tài liệu Dạy - học Toán lớp 9, Phát triển tư duy đột phá trong dạy học Toán 9 3. Liên hệ giữa dây và khoảng cách từ tâm đến dây

Thử tài bạn 5 trang 127 Tài liệu dạy – học Toán 9 tập 1


Giải bài tập Cho ABC là tam giác cân có góc đỉnh A

Đề bài

Cho ABC là tam giác cân có góc đỉnh A bằng \({30^o}\), nội tiếp đường tròn tâm O. Từ O hạ các đường thẳng vuông góc OM và ON xuống các cạnh tương ứng AB và BC.

Chứng minh OM < ON.

Lời giải chi tiết

 

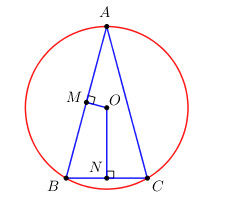
 Do \(\Delta ABC\) cân tại \(A \Rightarrow \widehat B = \widehat C\).

Mà \(\widehat A + \widehat B + \widehat C = {180^0}\) (tổng ba góc trong một tam giác)

\( \Rightarrow {30^0} + 2\widehat B = {180^0} \Leftrightarrow 2\widehat B = {150^0}\)

\(\Leftrightarrow \widehat B = {75^0} = \widehat C\).

Ta có \(\widehat A < \widehat C \Rightarrow BC < AB\) (trong một tam giác, cạnh đối diện với góc lớn hơn thì lớn hơn).

\( \Rightarrow OM < ON\) (trong một đường tròn, dây lớn hơn thì gần tâm hơn).

 Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store