-
CHƯƠNG I : CĂN BẬC HAI - CĂN BẬC BA
-
CHƯƠNG II : HÀM SỐ BẬC NHẤT
-
CHƯƠNG III: HỆ PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
-
CHƯƠNG IV: HÀM SỐ BẬC HAI VÀ PHƯƠNG TRÌNH BẬC HAI
-
CHƯƠNG I: HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
-
Chủ đề 1 : Một số hệ thức về cạnh và đường cao trong tam giác vuông
- 1. Hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền
- 2. Hệ thức giữa ba cạnh của tam giác vuông
- 3. Hệ thức giữa đường cao ứng với cạnh huyền và hình chiếu của hai cạnh góc vuông trên cạnh huyền
- 4. Hệ thức diện tích
- 5. Hệ thức giữa đường cao và hai cạnh góc vuông
- Bài tập - Chủ đề 1 : Một số hệ thức về cạnh và đường cao trong tam giác vuông
- Luyện tập - Chủ đề 1 : Một số hệ thức về cạnh và đường cao trong tam giác vuông
-
Chủ đề 2 : Tỉ số lượng giác của góc nhọn
- 1. Khái niệm tỉ số lượng giác của một góc nhọn
- 2. Liên hệ giữa các tỉ số lượng giác của một góc
- 3. Tỉ số lượng giác của hai góc phụ nhau
- 4. Tỉ số lượng giác của các góc đặc biệt
- 5. Tìm tỉ số lượng giác bằng máy tính cầm tay
- Bài tập - Chủ đề 2 : Tỉ số lượng giác của góc nhọn
- Luyện tập – Chủ đề 2 : Tỉ số lượng giác của góc nhọn
-
Chủ đề 3: Hệ thức về cạnh và góc trong tam giác vuông
-
Chủ đề 4 : Ứng dụng của tỉ số lượng giác
-
Ôn tập chương 1 - Hình học 9
-
-
CHƯƠNG II : ĐƯỜNG TRÒN
-
CHƯƠNG III: GÓC VỚI ĐƯỜNG TRÒN
Giải bài tập Tài liệu Dạy - học Toán lớp 9, Phát triển tư duy đột phá trong dạy học Toán 9
3. Liên hệ giữa dây và khoảng cách từ tâm đến dây
Hoạt động 6 trang 126 Tài liệu dạy – học Toán 9 tập 1
Giải bài tập Cho đường tròn (O ; 10 cm) và hai dây AB = 8 cm, CD = 6 cm. Từ O hạ OH và OK theo thứ tự
Tổng hợp Đề thi vào 10 có đáp án và lời giải
Toán - Văn - Anh
Đề bài
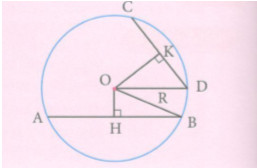
Cho đường tròn (O ; 10 cm) và hai dây AB = 8 cm, CD = 6 cm. Từ O hạ OH và OK theo thứ tự vuông góc với AB và CD.
Hãy tính OH, OK và cho biết đoạn nào dài hơn.
Lời giải chi tiết
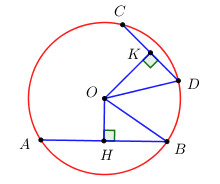
Ta có \(OH \bot AB,\,\,OK \bot CD \Rightarrow \) H, K theo thứ tự là trung điểm của \(AB,\,\,CD\).
\( \Rightarrow HB = \dfrac{1}{2}AB = \dfrac{1}{2}.8 = 4\,\,\left( {cm} \right),\)\(\,\,KD = \dfrac{1}{2}CD = \dfrac{1}{2}.6 = 3\,\,\left( {cm} \right)\)
Áp dụng định lí Pytago trong tam giác vuông \(OHB\) có:
\(O{H^2} = O{B^2} - H{B^2} = {10^2} - {4^2} = 84 \)
\(\Leftrightarrow OH = \sqrt {84} = 2\sqrt {21} \,\,\left( {cm} \right)\)
Áp dụng định lí Pytago trong tam giác vuông \(OKD\) có:
\(O{K^2} = O{D^2} - K{D^2} = {10^2} - {3^2} = 91\)
\(\Leftrightarrow OK = \sqrt {91} \,\,\left( {cm} \right)\)
Do \(91 > 84 \Rightarrow \sqrt {91} > \sqrt {84} \Rightarrow OK > OH\).
Vậy \(OK > OH\).
Loigiaihay.com
Bình luận
Chia sẻ
- Thử tài bạn 5 trang 127 Tài liệu dạy – học Toán 9 tập 1
- Hoạt động 7 trang 127 Tài liệu dạy – học Toán 9 tập 1
- Hoạt động 5 trang 126 Tài liệu dạy – học Toán 9 tập 1
- Thử tài bạn 4 trang 126 Tài liệu dạy – học Toán 9 tập 1
- Hoạt động 4 trang 125 Tài liệu dạy – học Toán 9 tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
