Luyện tập 4 trang 138 Tài liệu dạy – học Toán 8 tập 1

Đề bài

Cho hình bình hành ABCD có AB = 2AD. Gọi E, F lần lượt là trung điểm của AB và CD. Gọi I là giao điểm của AF và DE, K là giao điểm của BF và CE.

Chứng minh rằng:

a) Tứ giác AECF là hình bình hành.

b) Tứ giác AEFD là hình gì ? Vì sao ?

c) Chứng minh tứ giác EIFK là hình chữ nhật.

d) Tìm điều kiện của hình bình hành ABCD để tứ giác EIFK là hình vuông.

Lời giải chi tiết

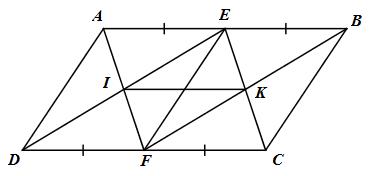
a) Ta có \(AE = EB = {{AB} \over 2}\) (E là trung điểm của AB),

\(DF = FC = {{CD} \over 2}\) (F là trung điểm của CD)

Và \(AB = CD\) (ABCD là hình bình hành)

\( \Rightarrow AE = CF = EB = DF\)

Tứ giác AECF có AE // CF (AB // CD, \(E \in AB,\,\,F \in CD\)) và \(AE = CF\)

\( \Rightarrow AECF\) là hình bình hành.

b) Ta có : \(AB = 2AD\,\,\left( {gt} \right)\)  và \(AB = 2AE\)  (E là trung điểm của AB) \) \Rightarrow AD = AE\)

Tứ giác AEFD có AE // DF và \(AE = DF\) (chứng minh câu a)

\( \Rightarrow \) Tứ giác AEFD là hình bình hành

Mà \(AE = AD\) (chứng minh trên) nên AEFD là hình thoi.

c) Ta có \(AF \bot DE\) tại I (AEFD là hình bình hành)

Và \(AF//EC\) (AECF là hình bình hành) \( \Rightarrow EC \bot DE \Rightarrow \widehat {IEK} = {90^0}\)

Ta có \(EF = AE\) (AEFD là hình thoi)

Và \(AE = {1 \over 2}AB\) (E là trung điểm của AB) \( \Rightarrow EF = {1 \over 2}AB\)

\(\Delta AFB\) có FE là đường trung tuyến (E là trung điểm của AB) và \(EF = {1 \over 2}AB\).

\( \Rightarrow \Delta AFB\) vuông tại F \( \Rightarrow \widehat {IFK} = {90^0}\)

Tứ giác EIFK có :

\(\widehat {EIF} = {90^0}\) (\(IE \bot IF\) tại I)

\(\eqalign{  & \widehat {IEK} = {90^0}\,\,\left( {cmt} \right)  \cr  & \widehat {IFK} = {90^0}\,\,\left( {cmt} \right) \cr} \)

Do đó tứ giác EIFK là hình chữ nhật.

d) Ta có tứ giác EIFK là hình chữ nhật.

I là trung điểm của ED (tứ giác AEFD là hình bình hành)

Tương tự K là trung điểm của EC.

Do đó IK là đường trung bình của tam giác ECD \( \Rightarrow IK \bot CD\)

Mặt khác AD // EF (tứ giác AEFD là hình bình hành)

Do đó tứ giác EIFK là hình vuông.

\( \Leftrightarrow \) Hình chữ nhật EIFK có \(IK \bot EF \Leftrightarrow IK \bot AD \Leftrightarrow AD \bot CD\)

\( \Leftrightarrow \) Hình bình hành ABCD có \(\widehat {ADC} = {90^0}\)

Vậy điều kiện của hình bình hành ABCD là \(\widehat {ADC} = {90^0}\) để tứ giác EIFK là hình vuông.

Loigiaihay.com