Luyện tập 3 trang 138 Tài liệu dạy – học Toán 8 tập 1

Giải bài tập Cho tam giác ABC vuông tại A (AB < AC). Gọi M, N, E lần lượt là trung điểm của AB, AC, BC.

Đề bài

Cho tam giác ABC vuông tại A (AB < AC). Gọi M, N, E lần lượt là trung điểm của AB, AC, BC.

a) Chứng minh tứ giác ANEB là hình thang vuông.

b) Chứng minh tứ giác ANEM là hình chữ nhật.

c) Đường thẳng song song với BN kẻ từ M cắt tia EN tại F. Chứng minh rằng tứ giác AFCE là hình thoi.

d) Gọi D là điểm đối xứng của E qua M. Chứng minh rằng A là trung điểm của DF.

Lời giải chi tiết

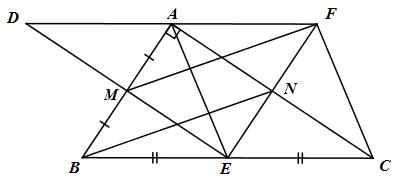
a) N, E lần lượt là trung điểm của AC và BC (gt);

$\Rightarrow NE$ là đường trung bình của tam giác ABC.

$\Rightarrow NE//AB \Rightarrow$ Tứ giác ANEB là hình thang.

Mà $\widehat {NAB} = {90^0}$ ( $\Delta ABC$ vuông tại A)

Do đó tứ giác ANEB là hình thang vuông.

b) M, E lần lượt là trung điểm của AB và BC (gt);

$\Rightarrow ME$ là đường trung bình của tam giác ABC $\Rightarrow ME//AC \Rightarrow ME//AN\,\,\left( {N \in AC} \right)$

Mà $AM//NE\,\,\left( {AB//NE,\,\,M \in AB} \right)$ nên tứ giác AMEN là hình bình hành.

Hình bình hành AMEN có $\widehat {MAN} = {90^0}$ nên là hình chữ nhật.

Tứ giác BMFN có: MF // BN (gt) và BM // FN (AB // NE, $M \in AB,\,\,F \in EN$ )

Do đó tứ giác BMFN là hình bình hành $\Rightarrow BM = FN$ .

Mặt khác $NE = AM$ (Tứ giác ANEM là hình chữ nhật) và $AM = BM$ . Do đó $FN = NE$ .

Tứ giác AFCE có N là trung điểm của AC, EF $\Rightarrow$ Tứ giác AFCE là hình bình hành.

Mà $AC \bot EF$ , do đó tứ giác AFCE là hình thoi (dấu hiệu nhận biết hình thoi)

d) Tứ giác ADBE có DE và AB cắt nhau tại M (gt)

M là trung điểm của AB (gt)

M là trung điểm của DE (D đối xứng với E qua M)

Do đó tứ giác ADBE là hình bình hành \) \Rightarrow AD//BE\)

Mà AF // EC ( do AECF là hình thoi) do đó AD, AF trùng nhau (tiên đề Ơ-clit)

$\Rightarrow A,D,F$ thẳng hàng $\Rightarrow A \in DF\,\,\left( 1 \right)$

Mặt khác, ADBE là hình bình hành

$\Rightarrow AF = EC$ (AECF là hinh thoi) và $BE = EC$ (E là trung điểm của BC) $\Rightarrow AD = AF\,\,\left( 2 \right)$

Từ (1) và (2) suy ra A là trung điểm của DF.

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

3.8 trên 8 phiếu

Bài tiếp theo

Luyện tập 4 trang 138 Tài liệu dạy – học Toán 8 tập 1
Giải bài tập Cho hình bình hành ABCD có AB = 2AD. Gọi E, F lần lượt là trung điểm của AB và CD. Gọi I là giao điểm của AF và DE, K là giao điểm của BF và CE.
Luyện tập 5 trang 138 Tài liệu dạy – học Toán 8 tập 1
Giải bài tập Cho hình bình hành ABCD vó AD = 2AB. Từ C vẽ CE vuông góc với AB. Nối E với trung điểm M của AD. Từ M vẽ MF vuông góc với CE, MF cắt BC tại N.
Luyện tập 6 trang 138 Tài liệu dạy – học Toán 8 tập 1
Giải bài tập Cho hình bình hành ABCD, tâm O. Trên đường chéo AC lấy hai điểm M, N sao cho AM = MN = CN.
Luyện tập 7 trang 138 Tài liệu dạy – học Toán 8 tập 1
Giải bài tập Cho hình bình hành ABCD. Lấy E, F trên AC sao cho AE = EF = FC.
Luyện tập 2 trang 138 Tài liệu dạy – học Toán 8 tập 1
Giải bài tập Cho tam giác ABC cân tại A. Họ H, D lần lượt là trung điểm của các cạnh BC và AB.
Luyện tập 1 trang 138 Tài liệu dạy – học Toán 8 tập 1
Giải bài tập Cho hình bình hành ABCD. Các điểm E, F thuộc đường chéo AC sao cho AE = EF = FC. Gọi M là giao điểm của BF và CD; N là giao điểm của DE và AB. Chứng minh rằng:

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

>> Học trực tuyến lớp 8 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả.