 Giải bài tập Tài liệu Dạy - học Toán lớp 8, Phát triển tư duy đột phá trong dạy học Toán 8
Giải bài tập Tài liệu Dạy - học Toán lớp 8, Phát triển tư duy đột phá trong dạy học Toán 8
 Luyện tập - Chủ đề 2 : Hình bình hành – Hình chữ nhật –..
Luyện tập - Chủ đề 2 : Hình bình hành – Hình chữ nhật –..
Luyện tập 1 trang 138 Tài liệu dạy – học Toán 8 tập 1
Giải bài tập Cho hình bình hành ABCD. Các điểm E, F thuộc đường chéo AC sao cho AE = EF = FC. Gọi M là giao điểm của BF và CD; N là giao điểm của DE và AB. Chứng minh rằng:
Đề bài
Cho hình bình hành ABCD. Các điểm E, F thuộc đường chéo AC sao cho \(AE = EF = FC.\) Gọi M là giao điểm của BF và CD; N là giao điểm của DE và AB. CHứng minh rằng:
a) M, N theo thứ tự là trung điểm của CD và AB.
b) Tứ giác EMFN là hình bình hành.
Lời giải chi tiết
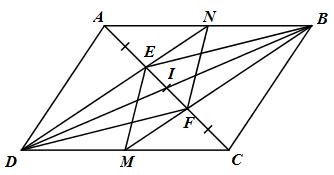
a) Gọi I là tâm đối xứng của hình bình hành ABCD
\( \Rightarrow I\) là trung điểm của AC và BD \( \Rightarrow IA = IC\)
\( \Rightarrow IA - AE = IC - FC\) (vì \(AE = FC\))
\( \Rightarrow EI = FI \Rightarrow I\) là trung điểm của EF.
Tứ giác DEBF có DB và EF cắt nhau tại I (I là tâm đối xứng, \(E,F \in AC\))
I là trung điểm của BD và I là trung điểm của EF.
Do đó tứ giác DEBF là hình bình hành
\( \Rightarrow DE//BF \Rightarrow EN//BF\,\,\left( {N \in DE} \right)\)
Mà E là trung điểm của AF \(\left( {AE = EF} \right)\) nên N là trung điểm của AB.
\(\Delta DEC\) có \(MF//DE\,\,\left( {DE//BF,\,\,M \in BF} \right)\) và F là trung điểm của EC \(\left( {EF = FC} \right)\)
\( \Rightarrow M\) là trung điểm của CD.
b) Ta có
\(AN = {{AB} \over 2}\) (N là trung điểm của AB)
\(MC = {{CD} \over 2}\) (M là trung điểm của CD)
\(AB = CD\) (ABCD là hình bình hành)
\( \Rightarrow AN = MC\)
Xét tam giác AEN và tam giác MFC ta có :
\(\eqalign{ & AE = FC\,\,\left( {gt} \right) \cr & AN = MC \cr} \)
\(\widehat {NAE} = \widehat {FCM}\) (hai góc so le trong và AB // CD)
Do đó \(\Delta AEN = \Delta CFM\,\,\left( {c.g.c} \right)\)
Tứ giác EMFN có EN // MF \(\left( {DE//BF,\,\,N \in DF,\,\,M \in BF} \right)\)
Và \(EN = MF\,\,\left( {\Delta AEN = \Delta CFM} \right)\). Do đó tứ giác EMFN là hình bình hành( Tứ giác có 2 cạnh đối song song và bằng nhau).
Loigiaihay.com












Danh sách bình luận