Bài 72 trang 169 SBT toán 9 tập 1

Giải bài 72 trang 169 sách bài tập toán 9. Cho hai đường tròn đồng tâm O. Gọi AB là dây bất kỳ của đường tròn nhỏ. Đường thẳng AB cắt đường tròn lớn ở C và D ( nằm giữa B và C). So sánh các độ dài AC và BD.

Đề bài

Cho hai đường tròn đồng tâm \(O.\) Gọi \(AB\) là dây bất kỳ của đường tròn nhỏ. Đường thẳng \(AB\) cắt đường tròn lớn ở \(C\) và \(D\) \((A\) nằm giữa \(B\) và \(C).\) So sánh các độ dài \(AC\) và \(BD.\)

Phương pháp giải - Xem chi tiết

Sử dụng kiến thức: Trong một đường tròn:

+) Đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.

Lời giải chi tiết

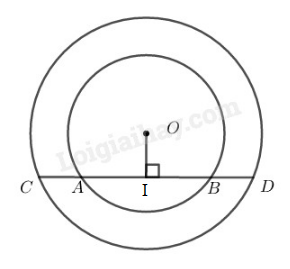
Kẻ \(OI ⊥ AB.\) Ta có: \(OI ⊥ CD\)

Trong đường tròn \((O)\) (nhỏ) ta có: \(OI ⊥ AB\)

Suy ra: \(IA = IB\) \((1)\) ( đường kính vuông góc dây cung thì đi qua trung điểm của dây ấy)

Trong đường tròn \((O)\) (lớn) ta có: \(OI ⊥ CD\)

Suy ra: \(IC = ID\) ( đường kính vuông góc dây cung thì đi qua trung điểm của dây ấy)

Hay \(IA + AC = IB + BD \) \( (2)\)

Từ \((1)\) và \((2)\) suy ra: \(AC = BD.\)

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.3 trên 8 phiếu

Bài tiếp theo

Bài 73 trang 169 SBT toán 9 tập 1
Giải bài 73 trang 169 sách bài tập toán 9. Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Gọi CD là tiếp tuyến chung ngoài của hai đường tròn ( C ∈ (O), D ∈ (O’))...
Bài 74 trang 169 SBT toán 9 tập 1
Giải bài 74 trang 169 sách bài tập toán 9. Cho hai đường tròn đồng tâm O. Một đường tròn (O’) cắt một đường tròn tâm O tại A, B và cắt đường tròn tâm O còn lại tại C, D. Chứng minh rằng AB // CD.
Bài 75 trang 169 SBT toán 9 tập 1
Giải bài 75 trang 169 sách bài tập toán 9. Cho đường tròn (O; 3cm) và đường tròn (O’; 1cm) tiếp xúc ngoài tại A. Vẽ hai bán kính OB và O’C song song với nhau thuộc cùng nửa mặt phẳng có bờ OO’...
Bài 76 trang 169 SBT toán 9 tập 1
Giải bài 76 trang 169 sách bài tập toán 9. Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ các đường kính AOB, AO’C. Gọi DE là tiếp tuyến chung của hai đường tròn, D ∈ (O), E ∈ (O’). Gọi M là giao điểm của BD và CE...
Bài 77* trang 169 SBT toán 9 tập 1
Giải bài 77* trang 169 sách bài tập toán 9. Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. kẻ tiếp tuyến chung ngoài MN với M thuộc (O) và N thuộc (O’). Gọi P là điểm đối xứng với M qua OO’, Q là điểm đối xứng với N qua OO’. Chứng minh rằng:...
Bài 78 trang 170 SBT toán 9 Tập 1
Giải bài 78 trang 170 sách bài tập toán 9. Cho đường tròn (O ; 2cm) và (O’ ; 3cm), OO’ = 6cm...
Bài 79 trang 170 SBT toán 9 tập 1
Giải bài 79 trang 170 sách bài tâp toán 9. Cho đường tròn (O ; R), điểm A nằm bên ngoài đường tròn (R < OA < 3R). Vẽ đường tròn (A ; 2R)...
Bài 80 trang 170 SBT toán 9 tập 1
Giải bài 80 trang 170 sách bài tập toán 9. Cho đường tròn (O ; 2cm) tiếp xúc với đường thẳng d. Dựng đường tròn (O’ ; 1cm) tiếp xúc với đường thẳng d và tiếp xúc ngoài đường tròn (O).
Bài 8.1 phần bài tập bổ sung trang 170 SBT toán 9 tập 1
Giải bài 8.1 phần bài tập bổ sung trang 170 sách bài tập toán 9. Cho hai đường tròn (O ; R) và (O' ; r). Điền vào chỗ trống của bảng sau:...
Bài 8.2 phần bài tập bổ sung trang 170 SBT toán 9 tập 1
Giải bài 8.2 phần bài tập bổ sung trang 170 sách bài tập toán 9. Cho hai đường tròn (O;3cm) và (O';4cm) có OO' = 5cm...
Bài 8.3 phần bài tập bổ sung trang 171 SBT toán 9 tập 1
Giải bài 8.3 phần bài tập bổ sung trang 171 sách bài tập toán 9. Cho đường tròn (O) và điểm A cố định trên đường tròn. Điểm B chuyển động trên đường tròn...
Bài 71 trang 168 SBT toán 9 tập 1
Giải bài 71 trang 168 sách bài tập toán 9. Cho I là trung điểm của đoạn thẳng AB. Vẽ các đường tròn (I ; IA) và (B ; BA)...