-
PHẦN ĐẠI SỐ - SBT TOÁN 7 TẬP 1
-
CHƯƠNG 1: SỐ HỮU TỈ. SỐ THỰC
- Bài 1. Tập hợp Q các số hữu tỉ
- Bài 2. Cộng, trừ số hữu tỉ
- Bài 3. Nhân, chia số hữu tỉ
- Bài 4. Giá trị tuyệt đối của một số hữu tỉ. Cộng, trừ, nhân, chia số thập phân
- Bài 5. Luỹ thừa của một số hữu tỉ
- Bài 6. Luỹ thừa của một số hữu tỉ (tiếp)
- Bài 7. Tỉ lệ thức
- Bài 8. Tính chất của dãy tỉ số bằng nhau
- Bài 9. Số thập phân hữu hạn. Số thập phân vô hạn tuần hoàn
- Bài 10. Làm tròn số
- Bài 11. Số vô tỉ. Khái niệm về căn bậc hai
- Bài 12. Số thực
- Ôn tập chương 1 - Số hữu tỉ. Số thực
-
CHƯƠNG 2: HÀM SỐ VÀ ĐỒ THỊ
- Bài 1. Đại lượng tỉ lệ thuận
- Bài 2. Một số bài toán về đại lượng tỉ lệ thuận
- Bài 3. Đại lượng tỉ lệ nghịch
- Bài 4. Một số bài toán về đại lượng tỉ lệ nghịch
- Bài 5. Hàm số
- Bài 6. Mặt phẳng toạ độ
- Bài 7. Đồ thị của hàm số y = ax (a khác 0)
- Ôn tập chương 2 - Hàm số và đồ thị
-
-
PHẦN HÌNH HỌC - SBT TOÁN 7 TẬP 1
-
CHƯƠNG 1: ĐƯỜNG THẲNG VUÔNG GÓC. ĐƯỜNG THẲNG SONG SONG
- Bài 1. Hai góc đối đỉnh
- Bài 2. Hai đường thẳng vuông góc
- Bài 3. Các góc tạo bởi một đường thẳng cắt hai đường thẳng
- Bài 4. Hai đường thẳng song song
- Bài 5. Tiên đề Ơ-clit về đường thẳng song song
- Bài 6. Từ vuông góc đến song song
- Bài 7. Định lí
- Ôn tập chương 1 - Đường thẳng vuông góc. Đường thẳng song song
-
CHƯƠNG 2: TAM GIÁC
- Bài 1. Tổng ba góc của một tam giác
- Bài 2. Hai tam giác bằng nhau
- Bài 3. Trường hợp bằng nhau thứ nhất của tam giác cạnh - cạnh - cạnh (c.c.c)
- Bài 4. Trường hợp bằng nhau thứ hai của tam giác cạnh - góc - cạnh (c.g.c)
- Bài 5. Trường hợp bằng nhau thứ ba của tam giác góc - cạnh - góc (g.c.g)
- Bài 6. Tam giác cân
- Bài 7. Định lí Py-ta-go
- Bài 8. Các trường hợp bằng nhau của tam giác vuông
- Bai 9: Thực hành ngoài trời
- Ôn tập chương 2 - Tam giác
-
-
PHẦN ĐẠI SỐ - SBT TOÁN 7 TẬP 2
-
CHƯƠNG 3: THỐNG KÊ
-
CHƯƠNG 4: BIỂU THỨC ĐẠI SỐ
- Bài 1. Khái niệm về biểu thức đại số
- Bài 2. Giá trị của biểu thức đại số
- Bài 3. Đơn thức
- Bài 4. Đơn thức đồng dạng
- Bài 5. Đa thức
- Bài 6. Cộng, trừ đa thức
- Bài 7. Đa thức một biến
- Bài 8. Cộng, trừ đa thức một biến
- Bài 9. Nghiệm của đa thức một biến
- Bài tập ôn chương 4 - Biểu thức đại số
-
-
PHẦN HÌNH HỌC - SBT TOÁN 7 TẬP 2
-
CHƯƠNG 3: QUAN HỆ GIỮA CÁC YẾU TỐ TRONG TAM GIÁC. CÁC ĐƯỜNG ĐỒNG QUY CỦA TAM GIÁC
- Bài 1. Quan hệ giữa góc và cạnh đối diện trong một tam giác
- Bài 2. Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
- Bài 3. Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức tam giác
- Bài 4. Tính chất ba đường trung tuyến của tam giác
- Bài 5. Tính chất tia phân giác của một góc
- Bài 6. Tính chất ba đường phân giác của tam giác
- Bài 7. Tính chất đường trung trực của một đoạn thẳng
- Bài 8. Tính chất ba đường trung trực của tam giác
- Bài 9. Tính chất ba đường cao của tam giác
- Bài tập ôn chương 3 - Quan hệ giữa các yếu tố trong tam giác. Các đường đồng quy trong tam giác
-
ÔN TẬP CUỐI NĂM
-
Bài 47 trang 143 SBT toán 7 tập 1
Giải bài 47 trang 143 sách bài tập toán 7 tập 1. Cho tam giác ABC có góc B = 2 góc C ...
Đề bài
Cho tam giác \(ABC\) có \(\widehat B = 2\widehat C\). Tia phân giác của góc \(B\) cắt \(AC\) ở \(D\). Trên tia đối của tia \(BD\) lấy điểm \(E\) sao cho \(BE = AC.\) Trên tia đối của tia \(CB\) lấy điểm \(K\) sao cho \(CK = AB.\) Chứng minh rằng \(AE = AK\).
Phương pháp giải - Xem chi tiết
- Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
- Tổng số đo hai góc kề bù bằng \(180^o\).
Lời giải chi tiết
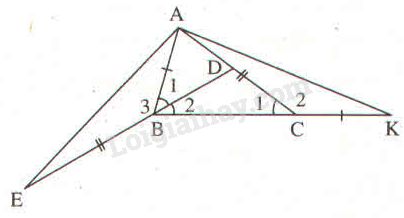
Ta có: \(\displaystyle \widehat B = 2\widehat {{C_1}}\left( {gt} \right) \Rightarrow \widehat {{C_1}} = {1 \over 2}\widehat B\)
Mặt khác: \(\displaystyle \widehat {{B_1}} = \widehat {{B_2}}={1 \over 2}\widehat B\) (vì \(BD\) là tia phân giác góc \(B\))
\( \Rightarrow \widehat {{C_1}} = \widehat {{B_1}}\) (1)
Lại có: \(\widehat {{C_1}} + \widehat {{C_2}} = 180^\circ \) (hai góc kề bù) (2)
\(\widehat {{B_1}} + \widehat {{B_3}} = 180^\circ \) (hai góc kề bù) (3)
Từ (1), (2) và (3) suy ra: \(\widehat {{C_2}} = \widehat {{B_3}}\)
Xét \(∆ABE\) và \(∆ KCA\), ta có:
\(AB = KC\) (gt)
\(\widehat {{B_3}} = \widehat {{C_2}}\) (chứng minh trên)
\(BE = CA\) (gt)
\( \Rightarrow ∆ABE = ∆ KCA\) (c.g.c)
\( \Rightarrow AE = AK\) (hai cạnh tương ứng).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 48 trang 143 SBT toán 7 tập 1
- Bài 4.1, 4.2, 4.3, 4.4 phần bài tập bổ sung trang 143, 144 SBT toán 7 tập 1
- Bài 46 trang 143 SBT toán 7 tập 1
- Bài 45 trang 143 SBT toán 7 tập 1
- Bài 44 trang 143 SBT toán 7 tập 1
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
