Bài 4.2 phần bài tập bổ sung trang 28 SBT toán 8 tập 1

Giải bài 4.1 phần bài tập bổ sung trang 28 sách bài tập toán 8. Viết tường minh hai phân thức đã cho và hai phân thức thu được sau khi quy đồng với mẫu thức chung

Đề bài

Cho hai phân thức \(\displaystyle {1 \over {{x^2} + ax - 2}}\), \(\displaystyle{2 \over {{x^2} + 5x + b}}\). Hãy xác định \(a\) và \(b\) biết rằng khi quy đồng mẫu thức chúng trở thành những phân thức có mẫu thức chung là \({x^3} + 4{x^2} + x - 6\). Viết tường minh hai phân thức đã cho và hai phân thức thu được sau khi quy đồng với mẫu thức chung là \({x^3} + 4{x^2} + x - 6\)

Phương pháp giải - Xem chi tiết

* Phép chia hết là phép chia có số dư bằng \(0\).

* Muốn quy đồng mẫu thức nhiều phân thức ta có thể làm như sau:

- Phân tích các mẫu thức thành nhân tử rồi tìm mẫu thức chung.

- Tìm nhân tử phụ của mỗi mẫu thức.

- Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng.

Lời giải chi tiết

Vì phép chia này là phép chia hết nên số dư phải bằng \(0\)

\( \Rightarrow 3-a\left( {4 - a} \right) = 0\) (1) và \(2 - 2a = 0\) (2)

Từ (2) ta có: \( 2 - 2a = a \Rightarrow a = 1\) và \(a = 1\) thỏa mãn (1).

Ta có phân thức \(\displaystyle {1 \over {{x^2} + x - 2}}\)

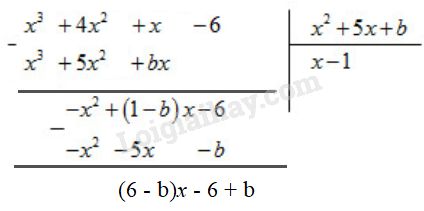
Vì phép chia này là phép chia hết nên số dư phải bằng \(0\).

\( \Rightarrow 6-b =0\) (3) và \( - 6 +b=0\) (4)

Từ (4) suy ra \( b = 6\) và \(b = 6\) cũng thỏa mãn (3).

Ta có phân thức \(\displaystyle {2 \over {{x^2} + 5x + 6}}\)

Khi đó:

\(\eqalign{ & +) \,{1 \over {{x^2} + x - 2}} \cr&= {{ {x + 3} } \over {\left( {{x^2} + x - 2} \right)\left( {x + 3} \right)}}\cr& = {{x + 3} \over {{x^3} + 4{x^2} + x - 6}} \cr & +)\,{2 \over {{x^2} + 5x + 6}} \cr&= {{2\left( {x - 1} \right)} \over {\left( {{x^2} + 5x + 6} \right)\left( {x - 1} \right)}} \cr&= {{2x - 2} \over {{x^3} + 4{x^2} + x - 6}} \cr} \)

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

3.7 trên 3 phiếu

Bài tiếp theo

Bài 4.1 phần bài tập bổ sung trang 28 SBT toán 8 tập 1
Giải bài 4.1 phần bài tập bổ sung trang 28 sách bài tập toán 8. Quy đồng mẫu thức ba phân thức ...
Bài 16 trang 28 SBT toán 8 tập 1
Giải bài 16 trang 28 sách bài tập toán 8. Hãy quy đồng mẫu thức. Cho hai phân thức ...
Bài 15 trang 28 SBT toán 8 tập 1
Giải bài 15 trang 28 sách bài tập toán 8. Cho đa thức B = 2.x^3 + 3.x^2 - 29x + 30 ...
Bài 14 trang 27 SBT toán 8 tập 1
Giải bài 14 trang 27 sách bài tập toán 8. Quy đồng mẫu thức các phân thức ...
Bài 13 trang 27 SBT toán 8 tập 1
Giải bài 13 trang 27 sách bài tập toán 8. Quy đồng mẫu thức các phân thức...