Bài 16 trang 28 SBT toán 8 tập 1

Giải bài 16 trang 28 sách bài tập toán 8. Hãy quy đồng mẫu thức. Cho hai phân thức ...

Đề bài

Cho hai phân thức \(\displaystyle {1 \over {{x^2} - 4x - 5}}\) và \(\displaystyle {2 \over {{x^2} - 2x - 3}}\)

Chứng tỏ rằng có thể chọn đa thức \({x^3} - 7{x^2} + 7x + 15\) làm mẫu thức chung để quy đồng mẫu thức hai phân thức đã cho. Hãy quy đồng mẫu thức.

Phương pháp giải - Xem chi tiết

Thực hiện phép chia đa thức \({x^3} - 7{x^2} + 7x + 15\) cho hai đa thức \({{x^2} - 4x - 5}\) và \({{x^2} - 2x - 3}\). Nếu các phép chia đều là phép chia hết thì đa thức \({x^3} - 7{x^2} + 7x + 15\) là mẫu thức chung để quy đồng mẫu thức hai phân thức đã cho.

Lời giải chi tiết

Ta có:

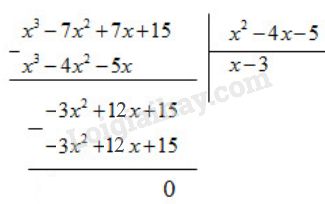
Suy ra: \({x^3} - 7{x^2} + 7x + 15 \)\(\,= \left( {{x^2} - 4x - 5} \right)\left( {x - 3} \right)\)

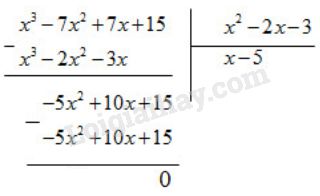
Suy ra: \({x^3} - 7{x^2} + 7x + 15 \)\(\,= \left( {{x^2} - 2x - 3} \right)\left( {x - 5} \right)\)

Vậy đa thức \({x^3} - 7{x^2} + 7x + 15\) là mẫu thức chung để quy đồng mẫu thức hai phân thức đã cho.

* Quy đồng:

\(\displaystyle {1 \over {{x^2} - 4x - 5}}\)

\(\displaystyle= {{1.\left( {x - 3} \right)} \over {\left( {{x^2} - 4x - 5} \right).\left( {x - 3} \right)}}\)

\(\displaystyle= {{x - 3} \over {{x^3} - 7{x^2} + 7x + 15}}\)

\(\displaystyle{2 \over {{x^2} - 2x - 3}} \)

\(\displaystyle= {{2.\left( {x - 5} \right)} \over {\left( {{x^2} - 2x - 3} \right)\left( {x - 5} \right)}} \)

\(\displaystyle= {{2\left( {x - 5} \right)} \over {{x^3} - 7{x^2} + 7x + 15}} \)

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.4 trên 11 phiếu

Bài tiếp theo

Bài 4.1 phần bài tập bổ sung trang 28 SBT toán 8 tập 1
Giải bài 4.1 phần bài tập bổ sung trang 28 sách bài tập toán 8. Quy đồng mẫu thức ba phân thức ...
Bài 4.2 phần bài tập bổ sung trang 28 SBT toán 8 tập 1
Giải bài 4.1 phần bài tập bổ sung trang 28 sách bài tập toán 8. Viết tường minh hai phân thức đã cho và hai phân thức thu được sau khi quy đồng với mẫu thức chung
Bài 15 trang 28 SBT toán 8 tập 1
Giải bài 15 trang 28 sách bài tập toán 8. Cho đa thức B = 2.x^3 + 3.x^2 - 29x + 30 ...
Bài 14 trang 27 SBT toán 8 tập 1
Giải bài 14 trang 27 sách bài tập toán 8. Quy đồng mẫu thức các phân thức ...
Bài 13 trang 27 SBT toán 8 tập 1
Giải bài 13 trang 27 sách bài tập toán 8. Quy đồng mẫu thức các phân thức...