Bài 4.1, 4.2, 4.3 phần bài tập bổ sung trang 43, 44 SBT toán 7 tập 2

Bài 4.1

Cho tam giác $ABC.$ Trên đường trung tuyến $AM$ của tam giác đó, lấy hai điểm $D, E$ sao cho $AD = DE = EM.$ Gọi $O$ là trung điểm của đoạn thẳng $DE.$ Khi đó trọng tâm của tam giác $ABC$ là:

(A) Điểm $D$               (B) Điểm $E$

(C) Điểm $O$               (D) Cả (A), (B), (C) đều sai

Phương pháp giải:

Sử dụng tính chất: Ba đường trung tuyến của tam giác cùng đi qua một điểm. Điểm đó cách đỉnh một khoảng bằng $\dfrac{2}{3}$ độ dài đường trung tuyến đi qua đỉnh ấy.

Lời giải chi tiết:

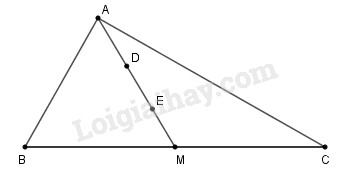
Do khoảng cách từ trọng tâm tới một đỉnh của tam giác bằng $\displaystyle {2 \over 3}$ độ dài đường trung tuyến đi qua đỉnh đó mà $AD=DE=EM$ nên $AE=\dfrac{2}{3}AM$, do đó $E$ là trọng tâm của tam giác $ABC.$

Chọn (B).

Bài 4.2

Cho tam giác $\displaystyle ABC,$ trên đường trung tuyến $\displaystyle AD.$ Gọi $\displaystyle G$ là điểm nằm giữa $\displaystyle A$ và $\displaystyle D$ sao cho $\displaystyle {{AG} \over {A{\rm{D}}}} = {2 \over 3}$. Tia $\displaystyle BG$ cắt $\displaystyle AC$ tại $\displaystyle E,$ tia $\displaystyle CG$ cắt $\displaystyle AB$ tại $\displaystyle F.$ Khẳng định nào sau đây sai?

$\displaystyle \left( A \right){{BG} \over {EG}} = 2$ 

$\displaystyle \left( B \right){{FG} \over {CG}} = {2 \over 3}$

(C) $\displaystyle E$ là trung điểm của cạnh $\displaystyle AC$

(D) $\displaystyle F$ là trung điểm của cạnh $\displaystyle AB$

Phương pháp giải:

Sử dụng tính chất: Ba đường trung tuyến của tam giác cùng đi qua một điểm. Điểm đó cách đỉnh một khoảng bằng $\displaystyle \dfrac{2}{3}$ độ dài đường trung tuyến đi qua đỉnh ấy. 

Lời giải chi tiết:

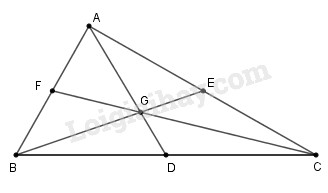
Do ba đường trung tuyến của một tam giác quy đồng tại trọng tâm của tam giác và trọng tâm cách mỗi đỉnh một khoảng bằng $\displaystyle {2 \over 3}$ độ dài đường trung tuyến đi qua đỉnh đó nên từ giả thiết suy ra $\displaystyle G$ là trọng tâm tam giác $\displaystyle ABC$

Vì $G$ là trọng tâm tam giác $\displaystyle ABC$ nên $BE$ là đường trung tuyến, suy ra E là trung điểm cạnh AC và $\displaystyle BG=\dfrac{2}{3} BE \Rightarrow \dfrac{BG}{EG} =2$

Vì $G$ là trọng tâm tam giác $\displaystyle ABC$ nên $\displaystyle CF$ là đường trung tuyến của tam giác $\displaystyle ABC$, suy ra $\displaystyle CG=\dfrac{2}{3} CF$ và $F$ là trung điểm của cạnh AB.

Từ đó: $\displaystyle FG=\dfrac{1}{3} CF$, suy ra $\displaystyle FG=\dfrac{1}{2} CG$ hay $\displaystyle \dfrac{FG}{CG}=\dfrac{1}{2}$

Hay (B) sai. 

Chọn $\displaystyle \left( B \right){{FG} \over {CG}} = {2 \over 3}$

Bài 4.3

Hai đoạn thẳng $\displaystyle AB$ và $\displaystyle CD$ cắt nhau tại trung điểm của mỗi đoạn. Gọi $\displaystyle E$ và $\displaystyle F$ theo thứ tự là trung điểm của các đoạn thẳng $\displaystyle AD$ và $\displaystyle BD.$ Các đoạn thẳng $\displaystyle CE$ và $\displaystyle CF$ lần lượt cắt đoạn thẳng $\displaystyle AB$ tại $\displaystyle I, J.$ Chứng minh rằng: $\displaystyle AI = IJ = JB.$

Phương pháp giải:

Sử dụng tính chất: Ba đường trung tuyến của tam giác cùng đi qua một điểm. Điểm đó cách đỉnh một khoảng bằng $\displaystyle \dfrac{2}{3}$ độ dài đường trung tuyến đi qua đỉnh ấy. 

Lời giải chi tiết:

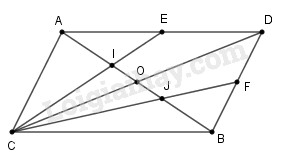
Gọi $\displaystyle O$ là giao điểm của hai đoạn thẳng $\displaystyle AB$ và $\displaystyle CD.$

$⇒ AO = OB$ và $CO = OD.$

+) $ΔACD$ có hai đường trung tuyến $AO, CE$ cắt nhau tại I

$⇒ I$ là trọng tâm $ΔACD$

Do đó: $\displaystyle OI = {1 \over 3}AO,AI = {2 \over 3}AO$ (1) (tính chất trọng tâm)

+) $ΔBCD$ có hai đường trung tuyến $BO, CF$ cắt nhau tại J

$⇒ J$ là trọng tâm $ΔBCD$

Do đó: $\displaystyle {\rm{OJ}} = {1 \over 3}BO,BJ = {2 \over 3}BO$ (2) (tính chất trọng tâm)

Từ (1), (2) và theo giả thiết $\displaystyle AO = BO$, ta có:

$\displaystyle {\rm{IJ}} = OI + {\rm{OJ}}= {1 \over 3}AO+{1 \over 3}BO$$\displaystyle = {1 \over 3}AO+{1 \over 3}AO$$=\displaystyle {2 \over 3}{\rm{AO = AI = BJ}}$

Vậy $\displaystyle AI = IJ = JB.$

Loigiaihay.com