Bài 4. Tính chất ba đường trung tuyến của tam giác

Bài 38 trang 43 SBT toán 7 tập 2

Giải bài 38 trang 43 sách bài tập toán 7. Cho tam giác ABC vuông tại A, đường trung tuyến AM. Trên tia đối của tia MA lấy điểm M sao cho MD = MA. a) Tính số đo góc ABD...

Đề bài

Cho tam giác \(ABC\) vuông tại \(A,\) đường trung tuyến \(AM.\) Trên tia đối của tia \(MA\) lấy điểm \(D\) sao cho \(MD = MA.\)

a) Tính số đo góc \(ABD.\)

b) Chứng minh: \(∆ABC = ∆BAD.\)

c) So sánh độ dài \(AM\) và \(BC.\)

Phương pháp giải - Xem chi tiết

Chứng minh hai tam giác bằng nhau theo trường hợp cạnh góc cạnh

Sử dụng quan hệ từ vuông góc đến song song.

Lời giải chi tiết

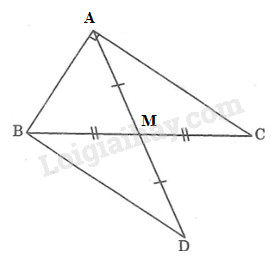
a) Vì \(AM\) là đường trung tuyến của tam giác \(ABC\) nên \(M\) là trung điểm của \(BC\)

Do đó: \(BM=MC\)

Xét \(\displaystyle ∆AMC\) và \(\displaystyle ∆DMB\) có:

+) \(\displaystyle BM = MC\) (chứng minh trên )

+) \(\displaystyle \widehat {AMC} = \widehat {BMD}\) (đối đỉnh)

+) \(\displaystyle AM = MD\) (gt)

Do đó: \(\displaystyle ∆AMC = ∆DMB\) (c.g.c)

\(\displaystyle \Rightarrow \widehat {MAC} = \widehat D\) (2 góc tương ứng)

Suy ra: \(\displaystyle AC // BD\) (vì có hai góc ở vị trí so le trong bằng nhau)

Mà \(\displaystyle AB \bot AC\left( {gt} \right)\)

Suy ra \(\displaystyle AB \bot B{\rm{D}}\). Vậy \(\displaystyle \widehat {AB{\rm{D}}} = 90^\circ \)

b) Xét \(\displaystyle ∆ABC\) và \(\displaystyle ∆BAD:\)

+) \(\displaystyle AB\) cạnh chung

+) \(\displaystyle \widehat {BAC} = \widehat {AB{\rm{D}}} = 90^\circ \)

+) \(\displaystyle AC = BD\) (vì \(\displaystyle ∆AMC = ∆DMB)\)

Do đó: \(\displaystyle ∆ABC = ∆BAD\) (c.g.c)

c) Vì \(\displaystyle ∆ABC = ∆BAD\) (chứng minh trên) nên \(\displaystyle BC = AD\) (2 cạnh tương ứng)

Ta có: \(\displaystyle AM = {1 \over 2}A{\rm{D}}\).

Suy ra: \(\displaystyle {\rm{A}}M = {1 \over 2}BC\)

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.4 trên 14 phiếu

Bài tiếp theo

Bài 39 trang 43 SBT toán 7 tập 2
Giải bài 39 trang 43 sách bài tập toán 7. Tam giác ABC có đường trung tuyến AM bằng nửa cạnh BC. Chứng minh rằng góc BAC bằng 90 độ.
Bài 4.1, 4.2, 4.3 phần bài tập bổ sung trang 43, 44 SBT toán 7 tập 2
Giải bài 4.1, 4.2, 4.3 phần bài tập bổ sung trang 43, 44 sách bài tập toán 7. Cho tam giác ABC. Trên đường trung tuyến AM của tam giác đó, lấy hai điểm D, E sao cho AD = DE = EM. Gọi O là trung điểm của đoạn thẳng DE. Khi đó trọng tâm của tam giác ABC là:...
Bài 4.4, 4.5, 4.6 phần bài tập bổ sung trang 44 SBT toán 7 tập 2
Giải bài 4.4, 4.5, 4.6 phần bài tập bổ sung trang 44 sách bài tập toán 7. Trong tam giác ABC, hai đường trung tuyến AA1 và BB1 cắt nhau tại điểm O. Hãy tính diện tích tam giác ABC nếu diện tích tam giác ABO bằng 5cm^2.
Bài 37 trang 43 SBT toán 7 tập 2
Giải bài 37 trang 43 sách bài tập toán 7. Cho tam giác ABC, đường trung tuyến AD. Kẻ đường trung tuyến BE cắt AD ở G. Gọi I, K theo thứ tự là trung điểm của GA, GB. Chứng minh rằng: a) IK // DE, IK = DE ...
Bài 36 trang 43 SBT toán 7 tập 2
Giải bài 36 trang 43 sách bài tập toán 7. Cho tam giác ABC. Trên tia đối của tia BA lấy điểm D sao cho BD = BA. Trên cạnh BC lấy điểm E sao cho...
Bài 35 trang 42 SBT toán 7 tập 2
Giải bài 35 trang 42 sách bài tập toán 7. Tam giác ABC có BC = 10cm, các đường trung tuyến BD và CE. Chứng minh rằng BD + CE > 15cm.
Bài 34 trang 42 SBT toán 7 tập 2
Giải bài 34 trang 42 sách bài tập toán 7.Gọi G là trọng tâm của tam giác ABC. Vẽ điểm D sao cho G là trung điểm của AD. Chứng minh rằng: a) Các cạnh của tam giác BGD bằng 2/3 các đường trung tuyến của tam giác ABC...
Bài 33 trang 42 SBT toán 7 tập 2
Giải bài 33 trang 42 sách bài tập toán 7. Tam giác ABC cân tại A có AB = AC = 34cm, BC = 32cm. Kẻ đường trung tuyến AM...
Bài 32 trang 42 SBT toán 7 tập 2
Giải bài 32 trang 42 sách bài tập toán 7. Chứng minh rằng nếu một tam giác có hai đường trung tuyến bằng nhau thì tam giác đó là tam giác cân.
Bài 31 trang 42 SBT toán 7 tập 2
Giải bài 31 trang 42 sách bài tập toán 7. Cho hình 7. Điền vào chỗ trống: GK = ….CK; AG = … GM; GK = … CG; AM = ….AG; AM = … GM.