-
PHẦN ĐẠI SỐ - SBT TOÁN 7 TẬP 1
-
CHƯƠNG 1: SỐ HỮU TỈ. SỐ THỰC
- Bài 1. Tập hợp Q các số hữu tỉ
- Bài 2. Cộng, trừ số hữu tỉ
- Bài 3. Nhân, chia số hữu tỉ
- Bài 4. Giá trị tuyệt đối của một số hữu tỉ. Cộng, trừ, nhân, chia số thập phân
- Bài 5. Luỹ thừa của một số hữu tỉ
- Bài 6. Luỹ thừa của một số hữu tỉ (tiếp)
- Bài 7. Tỉ lệ thức
- Bài 8. Tính chất của dãy tỉ số bằng nhau
- Bài 9. Số thập phân hữu hạn. Số thập phân vô hạn tuần hoàn
- Bài 10. Làm tròn số
- Bài 11. Số vô tỉ. Khái niệm về căn bậc hai
- Bài 12. Số thực
- Ôn tập chương 1 - Số hữu tỉ. Số thực
-
CHƯƠNG 2: HÀM SỐ VÀ ĐỒ THỊ
- Bài 1. Đại lượng tỉ lệ thuận
- Bài 2. Một số bài toán về đại lượng tỉ lệ thuận
- Bài 3. Đại lượng tỉ lệ nghịch
- Bài 4. Một số bài toán về đại lượng tỉ lệ nghịch
- Bài 5. Hàm số
- Bài 6. Mặt phẳng toạ độ
- Bài 7. Đồ thị của hàm số y = ax (a khác 0)
- Ôn tập chương 2 - Hàm số và đồ thị
-
-
PHẦN HÌNH HỌC - SBT TOÁN 7 TẬP 1
-
CHƯƠNG 1: ĐƯỜNG THẲNG VUÔNG GÓC. ĐƯỜNG THẲNG SONG SONG
- Bài 1. Hai góc đối đỉnh
- Bài 2. Hai đường thẳng vuông góc
- Bài 3. Các góc tạo bởi một đường thẳng cắt hai đường thẳng
- Bài 4. Hai đường thẳng song song
- Bài 5. Tiên đề Ơ-clit về đường thẳng song song
- Bài 6. Từ vuông góc đến song song
- Bài 7. Định lí
- Ôn tập chương 1 - Đường thẳng vuông góc. Đường thẳng song song
-
CHƯƠNG 2: TAM GIÁC
- Bài 1. Tổng ba góc của một tam giác
- Bài 2. Hai tam giác bằng nhau
- Bài 3. Trường hợp bằng nhau thứ nhất của tam giác cạnh - cạnh - cạnh (c.c.c)
- Bài 4. Trường hợp bằng nhau thứ hai của tam giác cạnh - góc - cạnh (c.g.c)
- Bài 5. Trường hợp bằng nhau thứ ba của tam giác góc - cạnh - góc (g.c.g)
- Bài 6. Tam giác cân
- Bài 7. Định lí Py-ta-go
- Bài 8. Các trường hợp bằng nhau của tam giác vuông
- Bai 9: Thực hành ngoài trời
- Ôn tập chương 2 - Tam giác
-
-
PHẦN ĐẠI SỐ - SBT TOÁN 7 TẬP 2
-
CHƯƠNG 3: THỐNG KÊ
-
CHƯƠNG 4: BIỂU THỨC ĐẠI SỐ
- Bài 1. Khái niệm về biểu thức đại số
- Bài 2. Giá trị của biểu thức đại số
- Bài 3. Đơn thức
- Bài 4. Đơn thức đồng dạng
- Bài 5. Đa thức
- Bài 6. Cộng, trừ đa thức
- Bài 7. Đa thức một biến
- Bài 8. Cộng, trừ đa thức một biến
- Bài 9. Nghiệm của đa thức một biến
- Bài tập ôn chương 4 - Biểu thức đại số
-
-
PHẦN HÌNH HỌC - SBT TOÁN 7 TẬP 2
-
CHƯƠNG 3: QUAN HỆ GIỮA CÁC YẾU TỐ TRONG TAM GIÁC. CÁC ĐƯỜNG ĐỒNG QUY CỦA TAM GIÁC
- Bài 1. Quan hệ giữa góc và cạnh đối diện trong một tam giác
- Bài 2. Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
- Bài 3. Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức tam giác
- Bài 4. Tính chất ba đường trung tuyến của tam giác
- Bài 5. Tính chất tia phân giác của một góc
- Bài 6. Tính chất ba đường phân giác của tam giác
- Bài 7. Tính chất đường trung trực của một đoạn thẳng
- Bài 8. Tính chất ba đường trung trực của tam giác
- Bài 9. Tính chất ba đường cao của tam giác
- Bài tập ôn chương 3 - Quan hệ giữa các yếu tố trong tam giác. Các đường đồng quy trong tam giác
-
ÔN TẬP CUỐI NĂM
-
Bài 31 trang 42 SBT toán 7 tập 2
Giải bài 31 trang 42 sách bài tập toán 7. Cho hình 7. Điền vào chỗ trống: GK = ….CK; AG = … GM; GK = … CG; AM = ….AG; AM = … GM.
Đề bài
Cho hình 7. Điền vào chỗ trống:
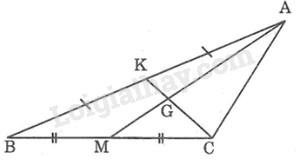
\(GK = ….CK; AG = … GM;\) \(GK = … CG;\)
\(AM = ….AG; AM = … GM.\)
Phương pháp giải - Xem chi tiết
Sử dụng tính chất:
Ba đường trung tuyến của tam giác cùng đi qua một điểm. Điểm đó cách đỉnh một khoảng bằng \(\dfrac{2}{3}\) độ dài đường trung tuyến đi qua đỉnh ấy.
Lời giải chi tiết
Từ hình vẽ ta thấy, \(AM, CK\) là hai đường trung tuyến của tam giác \(ABC\) và hai đường này cắt nhau tại \(G\) nên \(G\) là trọng tâm tam giác \(ABC\).
Suy ra: \(CG=\dfrac{2}{3}CK;AG=\dfrac{2}{3}AM\)
Do đó: \(\displaystyle GK = {1 \over 3}CK;AG = 2GM\)
\(\displaystyle GK = {1 \over 2}CG;AM = {3 \over 2}AG\)
\(AM = 3GM\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 32 trang 42 SBT toán 7 tập 2
- Bài 33 trang 42 SBT toán 7 tập 2
- Bài 34 trang 42 SBT toán 7 tập 2
- Bài 35 trang 42 SBT toán 7 tập 2
- Bài 36 trang 43 SBT toán 7 tập 2
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
