Bài 3.5, 3.6, 3.7, 3.8 phần bài tập bổ sung trang 54, 55 SBT toán 7 tập 2

Bài III.5

Cho tam giác \(ABC\) cân tại \(C.\) Kẻ các đường cao \({\rm{A}}{{\rm{A}}_1}\) và \(B{B_1}\) của tam giác đó. Hai đường cao này cắt nhau tại \(M.\) Chứng minh rằng đường thẳng \(MC\) là đường trung trực của đoạn thẳng \(AB.\)

Phương pháp giải:

Sử dụng:

+) Ba đường cao của tam giác động quy tại một điểm. Điểm đó là trực tâm tam giác.

+) Trong tam giác cân, đường cao xuất phát từ đỉnh cũng là đường trung trực của tam giác. 

Lời giải chi tiết:

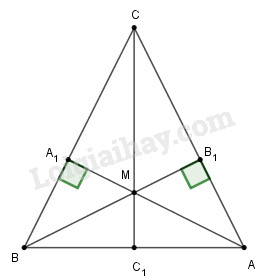
Xét tam giác \(ABC\) có hai đường cao \(AA_1\) và \(BB_1\) cắt nhau tại \(M\) nên \(M\) là trực tâm tam giác \(ABC.\) Do đó, \(CM\) là đường cao của tam giác \(ABC\) (vì trong một tam giác ba đường cao đồng quy)

Lại có tam giác \(ABC\) cân tại \(C\) nên đường cao \(CM\) cũng là đường trung trực của tam giác.

Vậy \(MC\) là đường trung trực của đoạn thẳng \(AB.\)

Bài III.6

Cho tam giác \(ABC\) có \(Â = 130°.\) Gọi \(C’, B’\) là các điểm sao cho \(AB\) là đường trung trực của \(CC’\) và \(AC\) là đường trung trực của \(BB’.\) Hai đường thẳng \(CB’\) và \(BC’\) cắt nhau tại \(A’.\) Hãy tìm bên trong tam giác \(A’BC\) điểm cách đều ba cạnh của tam giác đó.

Phương pháp giải:

Sử dụng:

+) Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.

+) Trong tam giác cân, đường trung trực ứng với cạnh đáy cũng là đường phân giác của tam giác.

+) Trong một tam giác, ba đường phân giác giao nhau tại một điểm. Điểm đó cách đều ba cạnh của tam giác.

Lời giải chi tiết:

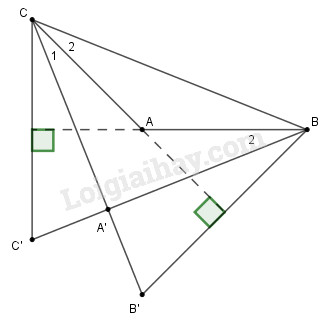
Xét tam giác \(A’BC\)

+) Vì \(AC\) là đường trung trực của \(BB’\) nên \(CB=CB'\) (tính chất đường trung trực)

Suy ra tam giác \(CBB'\) cân tại \(C\) có \(AC\) là đường trung trực nên \(AC\) cũng là đường phân giác của góc \(BCB'\)

+) Vì \(AB\) là đường trung trực của \(CC’\) nên \(BC=BC'\) (tính chất đường trung trực)

Suy ra tam giác \(BCC'\) cân tại \(B\) có \(AB\) là đường trung trực nên \(AB\) cũng là đường phân giác của góc \(CBC'\)

Suy ra \(AB, AC\) lần lượt là đường phân giác của các góc \(A’BC\) và góc \(A’CB.\) Vậy ba đường phân giác của tam giác \(A’BC\) đồng quy tại \(A,\) hay \(A\) là điểm nằm trong tam giác \(A’BC\) và cách đều ba cạnh của tam giác này.

Bài III.7

Dựng các hình vuông \(ABDE\) và \(ACFG\) bên ngoài tam giác nhọn \(ABC\) cho trước.

a) Gọi \(H\) là điểm thuộc đường thẳng \(BC\) sao cho \({\rm{A}}H \bot BC\). Gọi \(I, J \) là các điểm thuộc đường thẳng \(AH\) sao cho \(EI \bot AH\) và \(GJ \bot AH\). Chứng minh

\(∆ABH = ∆EAI, ∆ACH = ∆GAJ\)

Từ đó suy ra đường thẳng \(AH\) cắt \(EG\) tại trung điểm \(K\) của \(EG\) (tức là \(AK\) là trung tuyến của tam giác \(AEG)\)

b) Gọi \(L\) là điểm thuộc đường thẳng \(AK\) sao cho \(K\) là trung điểm của \(AL.\) Chứng minh \(AL = BC.\)

c) Chứng  minh \(∆ABL = ∆BDC.\) Từ đó suy ra \(CD\) là một đường cao của tam giác \(BCL.\)

d) Chứng minh rằng các đường thẳng \(AH, BF, CD\) đồng quy.

Phương pháp giải:

Sử dụng:

+) Các trường hợp bằng nhau của tam giác vuông

+) Ba đường cao của một tam giác đồng quy tại 1 điểm.

Lời giải chi tiết:

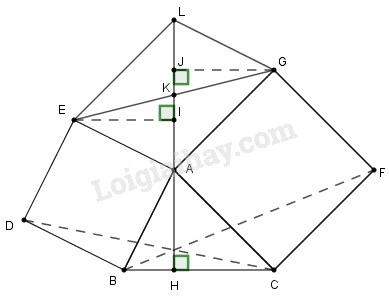
a) +) Xét tam giác EIA vuông tại I nên : \(\widehat {IEA} + \widehat {IAE} = {90^0}\) (tính chất tam giác vuông)

Lại có: \(\widehat {IAE} + \widehat {EAB} + \widehat {BAH} = {180^0}\) (1)

\( \Rightarrow \widehat {IAE} + \widehat {BAH} = {180^0} - \widehat {EAB} \)\(= {180^0} - {90^0} = {90^0}\)  (2)

Từ (1) và (2) suy ra \(\widehat {BAH} = \widehat {A{\rm{E}}I}\) (cùng phụ với góc \(EAI)\)

Hai tam giác vuông \(ABH\) và \(EAI\) có \(AB = EA,\) \(\widehat {BAH} = \widehat {A{\rm{E}}I}\) (chứng minh trên) nên \(∆ABH = ∆EAI\,\) (cạnh huyền-góc nhọn)

Suy ra \(AH=EI\) (hai cạnh tương ứng)

Tương tự hai tam giác vuông \(ACH\) và \(GAJ\) bằng nhau.

Suy ra \(AH=GJ\) (hai cạnh tương ứng)

Suy ra \(EI = AH = GJ.\)

Mặt khác, \(\widehat {JKG} = \widehat {IKE}\) (đối đỉnh), do đó  \(∆EKI = ∆GKJ\) (cgv-gn)

Từ đó ta có \(EK = GK,\) hay \(K\) là trung điểm của \(EG.\) Vậy \(AK\) là trung tuyến của tam giác \(AEG.\)

b) Theo a) \(∆EKI = ∆GKJ\) nên \(KI = KJ.\) Mặt khác, theo giả thiết \(K\) là trung điểm của \(AL\) nên \(AK = LK. \) Suy ra, \(KA – KI = KL – KJ\) hay \(IA= JL.\)

Ta có: \(∆ACH= ∆ GAJ\) ( theo a) nên \(HC = AJ\)

Lại có \(∆ABH = ∆ EAI\) (theo a) nên \(BH = AI.\)

Ta có:

\(AL = AJ + JL = AJ + AI \)\(= HC + HB  = BC\)

c) Hai tam giác \(ALB\) và \(BCD\) có

\(AL = BC\) (theo câu b)

\( AB = BD\)  ( vì ABDE là hình vuông)

\(\widehat {BAL} = 90^\circ  + \widehat {E{\rm{A}}L} \)\(= 90^\circ  + \widehat {ABC} = \widehat {DBC}\)

Nên \(∆ABL = ∆BCD\,(c-g-c)\)

Suy ra \(\widehat {ALB} = \widehat {BC{\rm{D}}}\).

Mặt khác ta có \(\widehat {ALB} + \widehat {LBH} = 90^\circ \) nên \(\widehat {BC{\rm{D}}} + \widehat {LBH} = 90^\circ \).

Suy ra \(LB \bot C{\rm{D}}\), tức \(CD\) là một đường cao của tam giác \(LBC.\)

d) Lập luận tương tự câu c), ta có \(BF\) là một đường cao của tam giác \(LBC.\)

Theo câu c) thì \(CD\) là một đường cao của tam giác \(LBC.\)

Vậy ba đường thẳng \(AH, BF, CD\) là ba đường cao của tam giác \(LBC\) nên chúng đồng quy.

Bài III.8

Cho tam giác \(ABC.\)

a) Qua trung điểm \(D\) của cạnh \(BC,\) kẻ đường thẳng song song với \(AB,\) nó cắt cạnh \(AC\) tại \(E.\) Qua \(E\) kẻ đường thẳng song song với \(BC,\) nó cắt \(AB\) tại \(F.\) Chứng minh \(∆CDE = ∆EFA.\) Từ đó suy ra \(E \) là trung điểm của cạnh \(AC.\) 

b) Chứng minh rằng đường thẳng đi qua các trung điểm hai cạnh của một tam giác thì song song với cạnh thứ ba của tam giác đó.

c) Chứng minh rằng tâm đường tròn ngoại tiếp tam giác \(ABC\) là trực tâm của tam giác có ba đỉnh là trung điểm ba cạnh của tam giác \(ABC.\)

Phương pháp giải:

Sử dụng:

+) Các trường hợp bằng nhau của tam giác

+) Tính chất hai đường thẳng song song

+) Tâm đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của tam giác đó

Lời giải chi tiết:

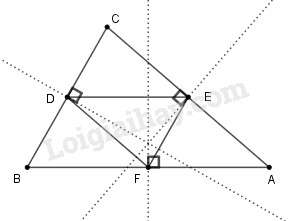
a) Xét \(∆BDF\) và \(∆EFD\) có:

+) \(\widehat {EDF} = \widehat {DFB}\) (so le trong, \(DE//AB)\)

+) \(DF\) cạnh chung

+) \(\widehat {EFD} = \widehat {FDB}\) (so le trong, \(EF//BC)\)

Ta có \(∆BDF = ∆EFD (g.c.g)\)

Suy ra \(BD = EF.\) Theo giả thiết, \(D\) là trung điểm của \(BC\) nên \(CD = DB = EF.\)

Hai tam giác \(CDE \) và \(EFA\) có:

+) \(\widehat {C{\rm{D}}E} = \widehat {CBA} = \widehat {{\rm{EFA}}}\) (các góc đồng vị)

+) \(CD = EF\)

+) \(\widehat {EC{\rm{D}}} = \widehat {{\rm{AEF}}}\) (các góc đồng vị)

Suy ra \(∆CDE = ∆EFA (g.c.g)\)

Do đó, \(CE = EA.\)

b) Ta có \(D\) là trung điểm của \(BC,\) \(E \) là trung điểm của \(AC.\) Theo câu a) đường thẳng qua \(D,\) song song với \(AB\) phải cắt \(AC\) tại trung điểm của \(AC\) nên đường thẳng đó phải đi qua \(E,\) hay \(DE // AB.\)

c) Gọi \(D, E, F\) theo thứ tự là trung điểm của \(BC, CA, AB.\) Đường trung trực của \(BC\) phải vuông góc với \(EF\) (vì (\(EF // BC),\) hay nó là một đường cao của tam giác \(DEF.\) Suy ra ba đường trung trực của tam giác \(ABC\) là ba đường cao của tam giác \(DEF.\) Do đó tâm đường tròn ngoại tiếp tam giác \(ABC\) (giao điểm của ba đường trung trực của tam giác \(ABC)\) là trực tâm của tam giác \(DEF.\)

Loigiaihay.com