Bài 3.1, 3.2, 3.3, 3.4 phần bài tập bổ sung trang 54 SBT toán 7 tập 2

Bài III.1

Chứng minh rằng trong một tam giác, đường cao không lớn hơn đường trung tuyến xuất phát từ một đỉnh.

Phương pháp giải:

Sử dụng:

Trong các đường xiên và đường vuông góc xuất phát từ một điểm đến một đường thẳng: Đường vuông góc luôn có độ dài nhỏ hơn đường xiên. 

Lời giải chi tiết:

Vì trong một tam giác, đường cao và đường trung tuyến xuất phát từ cùng một đỉnh lần lượt là đường vuông góc và đường xiên kẻ từ cùng một điểm đến cùng một đường thẳng mà đường vuông góc luôn nhỏ hơn đường xiên nên ta có đường cao luôn nhỏ hơn đường trung tuyến. (1)

Nếu đường cao và đường trung tuyến cùng xuất phát từ đỉnh của tam giác cân thì chúng bằng nhau. (2)

Vậy từ (1) và (2) ta suy ra trong một tam giác, đường cao không lớn hơn đường trung tuyến xuất phát từ một đỉnh.

Bài III.2

Cho tam giác \(ABC\) có hai đường trung tuyến \(AD, BE\) vuông góc với nhau. Chứng minh rằng \(BC < 2AC.\)

Phương pháp giải:

Sử dụng: 

+) Trong một tam giác, góc ngoài tại 1 đỉnh bằng tổng hai góc trong không kề với đỉnh đó.

+) Trong tam giác tù, đối diện với góc tù là cạnh có độ dài lớn nhất.

Lời giải chi tiết:

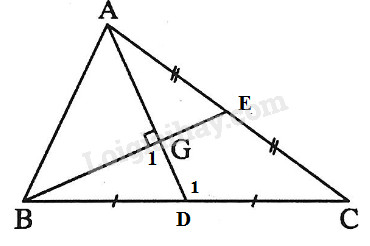
Xét hai tam giác \(ADC \) có \(\widehat {{D_1}} = \widehat {{G_1}} + \widehat {{GBD}}\) (góc ngoài tại 1 đỉnh bằng tổng hai góc trong không kề với đỉnh đó) 

Mà theo giả thiết \(\widehat {{G_1}} = 90^\circ \) nên \(\widehat {{D_1}}>90^0\) hay \(\widehat {{D_1}}\) là góc tù.

Trong tam giác \(ADC\) có \(\widehat {{D_1}}\) là góc tù và cạnh \(AC\) đối diện với góc \({{\rm{D}}_1}\) nên \(AC\) là cạnh lớn nhất trong tam giác (trong tam giác tù, đối diện với góc tù là cạnh có độ dài lớn nhất)

Nên \(AC > DC\).

Lại có \(D\) là trung điểm \(BC\) (do AD là đường trung tuyến của tam giác ABC) nên \(DC=\dfrac{BC}{2}\)

Từ đó \(AC > DC \)\(\Rightarrow AC>\dfrac{BC}{2}\) 

Do đó: \(2AC>BC\)

Bài III.3

Ba đường phân giác \(AD, BE, CF\) của tam giác \(ABC\) quy đồng tại \(O.\) Kẻ đường vuông góc \(OG\) đến \(BC. \) Chứng minh rằng \(\widehat {BOG} = \widehat {CO{\rm{D}}}\).

Phương pháp giải:

Sử dụng: 

+) Trong một tam giác, góc ngoài tại 1 đỉnh bằng tổng hai góc trong không kề với đỉnh đó.

+) Tổng ba góc trong tam giác bằng \(180^0\)

Lời giải chi tiết:

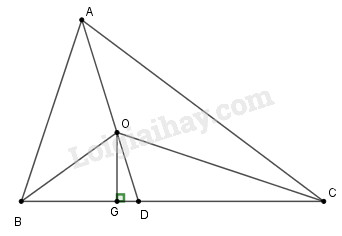
Để chứng minh \(\widehat {BOG} = \widehat {CO{\rm{D}}}\), ta chứng minh \(\widehat {BO{\rm{D}}} = \widehat {GOC}\).

Trong tam giác \(ABC\) có \(\widehat A + \widehat B + \widehat C = {180^0}\) (tổng ba góc trong tam giác) nên \(\widehat A + \widehat B = {180^0} - \widehat C\)

Xét tam giác ABC có AO, BO, CO lần lượt là phân giác các góc trong A, B, C

Nên \(\widehat {OAB} = \dfrac{1}{2}\widehat A,\widehat {OBA} = \dfrac{1}{2}\widehat B\), \(\widehat {OCG} = \dfrac{1}{2}\widehat C\)

Xét tam giác \(OAB,\) ta có \(\widehat {BO{\rm{D}}} \) là góc ngoài tại đỉnh O nên \(\widehat {BOD} = \widehat {OAB} + \widehat {OBD}\)

Suy ra \(\widehat {BO{\rm{D}}} \)\(\displaystyle= {1 \over 2}\left( {\widehat A + \widehat B} \right) \)\(\displaystyle = {1 \over 2}\left( {180^\circ  - \widehat C} \right)\)     (1)

Xét tam giác vuông \(OCG\) ta có: \(\widehat {GOC} + \widehat {OCG} = {90^0}\) (trong tam giác vuông, tổng hai góc nhọn bằng \(90^0\)) 

Nên \(\displaystyle \widehat {GOC} = {90^0}-\widehat {OCG}\)\(\displaystyle =90^\circ  - {1 \over 2}\widehat C \)\(\displaystyle = {1 \over 2}\left( {180^\circ  - \widehat C} \right)\)        (2)

Từ (1) và (2) suy ra \(\widehat {BO{\rm{D}}} = \widehat {GOC}\).

Do đó: \(\widehat {BOD} - \widehat {DOG} = \widehat {COG} - \widehat {DOG}\)

Hay \(\widehat {BOG} = \widehat {CO{\rm{D}}}\).

Bài III.4

Cho tam giác \(ABC\) cân tại \(B\) có \(\widehat B = 112^\circ \). Kẻ đường cao \(AH\) và đường phân giác \(AD\) của tam giác đó. Tính các góc của tam giác \(AHD.\)

Phương pháp giải:

Sử dụng:

+) Trong một tam giác, góc ngoài tại 1 đỉnh bằng tổng hai góc trong không kề với đỉnh đó.

+) Tổng ba góc trong tam giác bằng \(180^0.\)

+) Trong tam giác cân, hai góc kề cạnh đáy bằng nhau. 

Lời giải chi tiết:

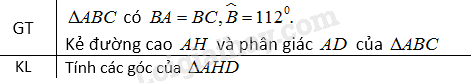
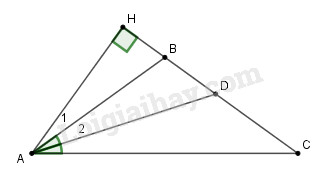
Ta có: \(\widehat {ABH} + \widehat {ABC} = {180^0}\) (hai góc kề bù)

Nên \(\widehat {ABH} = 180^\circ - \widehat {ABC}\)\(=180^\circ  - 112^\circ  = 68^\circ \)

Xét tam giác \(AHB\) vuông tại H, ta có: \(\widehat {{A_1}} + \widehat {ABH}= 90^\circ \)  ( tính chất tam giác vuông) nên \(\widehat {{A_1}} = 90^\circ  - \widehat {ABH} = 90^\circ  - 68^\circ  = 22^\circ \)

Tam giác \(ABC\) cân tại \(B\) nên \(\widehat {BAC} = \widehat {ACB}\) (tính chất)

Lại có \(\widehat B = 112^\circ \) và \(\widehat {BAC} + \widehat {ACB} + \widehat {ABC} = {180^0}\) (định lý về tổng ba góc trong tam giác) nên  \(\widehat {BAC} + \widehat {ACB} =180^0- \widehat {ABC} = {180^0}-112^0=68^0\) hay \(2.\widehat {BAC} =68^0\)

Từ đó \(\widehat {BAC} =68^0:2 = 34^\circ \)  

Do AD là tia phân giác của góc BAC nên \(\widehat {{A_2}} = \widehat {BAC}:2\)\( = 34^\circ :2 = 17^\circ \).

Từ đó: \(\widehat {HA{\rm{D}}} = \widehat {{A_1}} + \widehat {{A_2}} \)\(= 22^\circ  + 17^\circ  = 39^\circ \)

Xét tam giác \(HDA\) vuông tại \(H\) có: \(\widehat {H{\rm{D}}A} + \widehat {HA{\rm{D}}}= 90^\circ   \) (tính chất tam giác vuông) nên \(\widehat {H{\rm{D}}A} = 90^\circ  - \widehat {HA{\rm{D}}} \)\(= 90^\circ  - 39^\circ  = 51^\circ \)

Loigiaihay.com