Bài 28 trang 41 SBT toán 7 tập 2

Giải bài 28 trang 41 sách bài tập toán 7. Tính chu vi của một tam giác cân biết độ dài hai cạnh của nó bằng 3dm và 5dm.

Đề bài

Tính chu vi của một tam giác cân biết độ dài hai cạnh của nó bằng \(3dm\) và \(5dm.\)

Phương pháp giải - Xem chi tiết

Sử dụng:
Trong một tam giác:

+) Hiệu độ dài hai cạnh bất kỳ bao giờ cũng nhỏ hơn độ dài cạnh còn lại

+) Độ dài một cạnh bao giờ cũng nhỏ hơn tổng độ dài của hai cạnh còn lại

+) Chu vi tam giác bằng tổng độ dài ba cạnh của tam giác đó

Lời giải chi tiết

Vì tam giác cân hai cạnh bên bằng nhau.

Trong hai số đo \(3dm\) và \(5dm\) có một số đo độ dài cạnh bên và một số đo độ dài cạnh đáy.

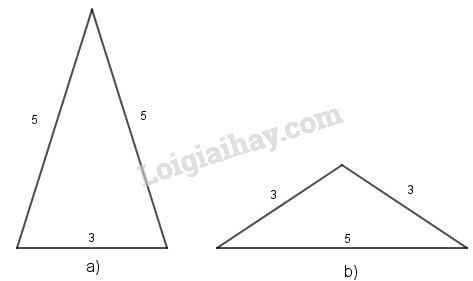
Nếu \(5dm\) là độ dài cạnh bên ta có: \(3 + 5 > 5\) và \(5 - 3 < 5 \) do đó tồn tại tam giác (Hình a)

Chu vi tam giác cân là: \(5 + 5 + 3 = 13\) (dm).

Nếu \(3dm\) là độ dài cạnh bên ta có: \(3 + 3 > 5\) và \(5 - 3 < 3 \) do đó tồn tại tam giác (Hình b)

Chu vi tam giác cân là: \(3 + 3 + 5 = 11\) (dm)

Bình luận

Chia sẻ

Bình chọn:

4.4 trên 15 phiếu

Bài tiếp theo

Bài 29 trang 41 SBT toán 7 tập 2
Giải bài 29 trang 41 sách bài tập toán 7. Độ dài hai cạnh của một tam giác bằng 7cm và 2cm. Tính độ dài cạnh còn lại biết rằng số đo của nó theo xentimét là một số tự nhiên lẻ.
Bài 30 trang 41 SBT toán 7 tập 2
Giải bài 30 trang 41 sách bài tập toán 7. Cho tam giác ABC. Gọi M là trung điểm của BC. Chứng minh rằng AM<(AB+AC)/2
Bài 3.1, 3.2, 3.3, 3.4 phần bài tập bổ sung trang 41, 42 SBT toán 7 tập 2
Giải bài 3.1, 3.2, 3.3, 3.4 phần bài tập bổ sung trang 41, 42 sách bài tập toán 7. Bộ ba nào sau đây không thể là số đo ba cạnh của một tam giác? (A) 1cm, 2m, 2,5cm (B) 3cm; 4cm ; 6cm; (C) 6cm, 7cm, 13cm; (D) 6cm, 7cm, 12cm
Bài 3.5, 3.6, 3.7 phần bài tập bổ sung trang 42 SBT toán 7 tập 2
Giải bài 3.5, 3.6, 3.7 phần bài tập bổ sung trang 42 sách bài tập toán 7. Chứng minh rằng trong một đường tròn, đường kính là dây lớn nhất.
Bài 27 trang 41 SBT toán 7 tập 2
Giải bài 27 trang 41 sách bài tập toán 7. Cho điểm M nằm trong tam giác ABC. Chứng minh rằng tổng MA + MB + MC lớn hơn nửa chu vi tam giác ABC.
Bài 26 trang 41 SBT toán 7 tập 2
Giải bài 26 trang 41 sách bài tập toán 7. Cho tam giác ABC, điểm D nằm giữa B và C. Chứng minh rằng AD nhỏ hơn nửa chu vi tam giác ABC.
Bài 25 trang 41 SBT toán 7 tập 2
Giải bài 25 trang 41 sách bài tập toán 7. Ba thành phố A, B C trên bản đồ là ba đỉnh của một tam giác, trong đó AC = 30km, AB = 70km a) Nếu đặt ở C máy phát sóng truyền thanh có bán kính hoạt động bằng 40km thì thành phố B có nhận được tín hiệu không? Vì sao?
Bài 24 trang 41 SBT toán 7 tập 2
Giải bài 24 trang 41 sách bài tập toán 7. Cho hai điểm A và B nằm về hai phía của đường thẳng d. Tìm điểm C thuộc đường thẳng d sao cho tổng AC + CB là nhỏ nhất.
Bài 23 trang 40 SBT toán 7 tập 2
Giải bài 23 trang 40 sách bài tập toán 7. Cho tam giác ABC trong đó BC là cạnh lớn nhất. a) Vì sao các góc B và C không thể là góc vuông hoặc góc tù? b) Gọi AH là đường vuông góc kẻ từ A đến BC. So sánh AB + AC với BH + CH rồi chứng minh rằng AB + AC > BC.
Bài 22 trang 40 SBT toán 7 tập 2
Giải bài 22 trang 40 sách bài tập toán 7. Tính chu vi của một tam giác cân có hai cạnh bằng 4m và 9m.
Bài 21 trang 40 SBT toán 7 tập 2
Giải bài 21 trang 40 sách bài tập toán 7. Cho hình 5. Chứng minh rằng MA + MB < IA + IB < CA + CB
Bài 20 trang 40 SBT toán 7 tập 2
Giải bài 20 trang 40 sách bài tập toán 7. Cho tam giác ABC có AB = 4cm; AC = 1cm. Hãy tìm độ dài cạnh BC biết rằng độ dài này là một số nguyên (cm).
Bài 19 trang 40 SBT toán 7 tập 2
Giải bài 19 trang 40 sách bài tập toán 7. Có thể có tam giác nào mà độ dài ba cạnh như sau không? a) 5cm; 10cm; 12cm? b) 1m; 2m; 3,3m? c) 1,2m; 1m; 2,2m?