Bài 20 trang 159 SBT toán 9 tập 1

Giải bài 20 trang 159 sách bài tập toán 9. Cho nửa đường tròn tâm O, đường kính AB, dây CD. Các đường vuông góc với CD tại C và D tương ứng cắt AB ở M và N. Chứng minh rằng AM = BN...

Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn

Đề bài

a) Cho nửa đường tròn tâm \(O\), đường kính \(AB\), dây \(CD\). Các đường vuông góc với \(CD\) tại \(C\) và \(D\) tương ứng cắt \(AB\) ở \(M\) và \(N\). Chứng minh rằng \(AM = BN.\)

b) Cho nửa đường tròn tâm \(O\), đường kính \(AB\). Trên \(AB\) lấy các điểm \(M, N\) sao cho \( AM = BN\). Qua \(M\) và qua \(N\), kẻ các đường thẳng song song với nhau, chúng cắt nửa đường tròn lần lượt ở \(C\) và \(D\). Chứng minh rằng \(MC\) và \(ND\) vuông góc với \(CD\).

Phương pháp giải - Xem chi tiết

+ Áp dụng định lí : Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.

+ Áp dụng đường trung bình của hình thang: Đường thẳng đi qua trung điểm hai cạnh bên của hình thang thì song song với hai đáy của hình thang đó.

Lời giải chi tiết

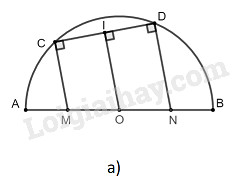
a) Ta có:

\(CM ⊥CD\)

\(DN⊥CD\)

Suy ra: \(CM // DN\)

Kẻ \(OI ⊥CD\)

Suy ra: \(OI // CM // DN\)

Xét (O) có \(OI ⊥CD\) mà OI là 1 phần đường kính và DC là dây của đường tròn nên \(IC = ID\) (đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy)

Hình thang MCDN (do \(CM // DN\)) có \(OI // CM // DN\) và \(IC=ID\)

Suy ra: \(OM = ON\) (1)

Mà: \(AM + OM = ON + BM( = R)\) (2)

Từ (1) và (2) suy ra: \(AM = BN.\)

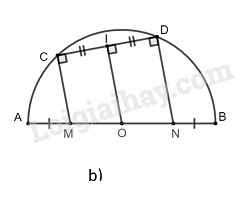
b) Ta có: \(MC // ND\) (gt)

Suy ra tứ giác \(MCDN\) là hình thang

Lại có: \(OM + AM = ON + BN (= R)\)

Mà \(AM = BN\) (gt)

Suy ra: \(OM = ON\)

Kẻ \(OI ⊥ CD \) (3)

Khi đó \(OI\) là đường trung bình của hình thang \(MCDN\) (vì \(OM = ON\) và \(IC = ID\))

Suy ra: \(OI // MC // ND\) (4)

Từ (3) và (4) suy ra: \(MC ⊥ CD, ND ⊥ CD.\)

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.4 trên 22 phiếu

Bài tiếp theo

Bài 21* trang 159 SBT toán 9 tập 1
Giải bài 21* trang 159 sách bài tập toán 9. Cho đường tròn tâm O, đường kính AB. Dây CD cắt đường kính AB tại I. Gọi H và K theo thứ tự là chân các đường vuông góc kẻ từ A và B đến CD. Chứng minh rằng CH = DK.
Bài 22 trang 159 SBT toán 9 tập 1
Giải bài 22 trang 159 sách bài tập toán 9. Cho đường tròn (O; R) và điểm M nằm bên trong đường tròn. a) Hãy nêu cách dựng dây AB nhận M làm trung điểm...
Bài 23 trang 159 SBT toán 9 tập 1
Giải bài 23 trang 159 sách bài tập toán 9. Cho đường tròn (O), điểm A nằm bên trong đường tròn, điểm B nằm ngoài đường tròn sao cho trung điểm I của AB nằm bên trong đường tròn. Vẽ dây CD vuông góc với OI tại I. hãy cho biết ACBD là hình gì? Vì sao?
Bài 2.1 phần bài tập bổ sung trang 159 SBT toán 9 tập 1
Giải bài 2.1 phần bài tập bổ sung trang 159 sách bài tập toán 9. Độ dài cạnh của tam giác đều nội tiếp đường tròn (O; R) bằng:
Bài 2.2 phần bài tập bổ sung trang 160 SBT toán 9 tập 1
Giải bài 2.2 phần bài tập bổ sung trang 160 sách bài tập toán 9. Cho đường tròn (O; 2cm). Vẽ hai dây AB và CD vuông góc với nhau. Tính diện tích lớn nhất của tứ giác ABCD.
Bài 2.3 phần bài tập bổ sung trang 160 SBT toán 9 tập 1
Giải bài 2.3 phần bài tập bổ sung trang 160 sách bài tập toán 9. Cho đường tròn (O; R), dây AB khác đường kính. Vẽ về hai phía của AB các dây AC, AD. Gọi H và K theo thứ tự là chân các đường vuông góc kẻ từ B và AC và AD. Chứng minh rằng:
Bài 19 trang 159 SBT toán 9 tập 1
Giải bài 19 trang 159 sách bài tập toán 9. Cho đường tròn (O), đường kính AD = 2R. Vẽ cung tâm D bán kính R, cung này cắt đường tròn (O) ở B và C...
Bài 18 trang 159 SBT toán 9 tập 1
Giải 18 trang 159 sách bài tập toán 9. Cho đường tròn (O) có bán kính OA = 3cm. Dây BC của đường tròn vuông góc với OA tại trung điểm của OA. Tính độ dài BC...
Bài 17 trang 159 SBT toán 9 tập 1
Giải bài 17 trang 159 sách bài tập toán 9. Cho nửa đường tròn tâm O, đường kính AB và dây EF không cắt đường kính. Gọi I và K lần lượt là chân các đường vuông góc kẻ từ A và B đến EF. Chứng minh rằng IE = KF.
Bài 16 trang 159 SBT toán 9 tập 1
Giải bài 16 trang 159 sách bài tập toán 9. Chứng minh rằng bốn điểm A, B, C, D cùng thuộc một đường tròn...
Bài 15 trang 158 SBT toán 9 tập 1
Giải bài 15 trang 158 sách bài tập toán 9. Cho tam giác ABC, các đường cao BH và CK. Chứng minh rằng: a) Bốn điểm B, C, H, K cùng thuộc một đường tròn;...