Bài 15 trang 158 SBT toán 9 tập 1

Giải bài 15 trang 158 sách bài tập toán 9. Cho tam giác ABC, các đường cao BH và CK. Chứng minh rằng: a) Bốn điểm B, C, H, K cùng thuộc một đường tròn;...

Đề bài

Cho tam giác \(ABC\), các đường cao \(BH\) và \(CK\). Chứng minh rằng:

a) Bốn điểm \(B, C, H, K\) cùng thuộc một đường tròn;

b) \(HK < BC.\)

Phương pháp giải - Xem chi tiết

+ Để chứng minh các điểm thuộc cùng một đường tròn ta chứng minh các điểm này cách đều một điểm.

+ Trong các dây của đường tròn, dây lớn nhất là đường kính.

Lời giải chi tiết

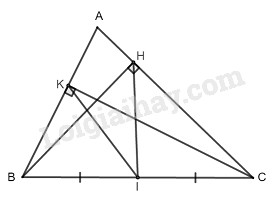
a) Gọi \(I\) là trung điểm của \(BC\)

Tam giác \(BCH\) vuông tại \(H\) có \(HI\) là đường trung tuyến nên: \(HI= IB=IC=\dfrac{1}{2}BC\) (tính chất tam giác vuông)

Tam giác \(BCK\) vuông tại \(K\) có \(KI\) là đường trung tuyến nên:

\(KI =IB=IC= \dfrac{1}{2}BC\) (tính chất tam giác vuông)

Suy ra: \(IB = IC = IH = IK=\dfrac{1}{2}BC.\)

Vậy bốn điểm \(B, C, H, K\) cùng nằm trên một đường tròn tâm \(I\) bán kính bằng \(\dfrac{1}{2}BC\).

b) Trong đường tròn tâm \(I\) bán kính \(\dfrac{1}{2}BC,\) ta có \(KH\) là dây cung không đi qua tâm, \(BC\) là đường kính nên: \(KH < BC\) (trong các dây của đường tròn, dây lớn nhất là đường kính).

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.7 trên 16 phiếu

Bài tiếp theo

Bài 16 trang 159 SBT toán 9 tập 1
Giải bài 16 trang 159 sách bài tập toán 9. Chứng minh rằng bốn điểm A, B, C, D cùng thuộc một đường tròn...
Bài 17 trang 159 SBT toán 9 tập 1
Giải bài 17 trang 159 sách bài tập toán 9. Cho nửa đường tròn tâm O, đường kính AB và dây EF không cắt đường kính. Gọi I và K lần lượt là chân các đường vuông góc kẻ từ A và B đến EF. Chứng minh rằng IE = KF.
Bài 18 trang 159 SBT toán 9 tập 1
Giải 18 trang 159 sách bài tập toán 9. Cho đường tròn (O) có bán kính OA = 3cm. Dây BC của đường tròn vuông góc với OA tại trung điểm của OA. Tính độ dài BC...
Bài 19 trang 159 SBT toán 9 tập 1
Giải bài 19 trang 159 sách bài tập toán 9. Cho đường tròn (O), đường kính AD = 2R. Vẽ cung tâm D bán kính R, cung này cắt đường tròn (O) ở B và C...
Bài 20 trang 159 SBT toán 9 tập 1
Giải bài 20 trang 159 sách bài tập toán 9. Cho nửa đường tròn tâm O, đường kính AB, dây CD. Các đường vuông góc với CD tại C và D tương ứng cắt AB ở M và N. Chứng minh rằng AM = BN...
Bài 21* trang 159 SBT toán 9 tập 1
Giải bài 21* trang 159 sách bài tập toán 9. Cho đường tròn tâm O, đường kính AB. Dây CD cắt đường kính AB tại I. Gọi H và K theo thứ tự là chân các đường vuông góc kẻ từ A và B đến CD. Chứng minh rằng CH = DK.
Bài 22 trang 159 SBT toán 9 tập 1
Giải bài 22 trang 159 sách bài tập toán 9. Cho đường tròn (O; R) và điểm M nằm bên trong đường tròn. a) Hãy nêu cách dựng dây AB nhận M làm trung điểm...
Bài 23 trang 159 SBT toán 9 tập 1
Giải bài 23 trang 159 sách bài tập toán 9. Cho đường tròn (O), điểm A nằm bên trong đường tròn, điểm B nằm ngoài đường tròn sao cho trung điểm I của AB nằm bên trong đường tròn. Vẽ dây CD vuông góc với OI tại I. hãy cho biết ACBD là hình gì? Vì sao?
Bài 2.1 phần bài tập bổ sung trang 159 SBT toán 9 tập 1
Giải bài 2.1 phần bài tập bổ sung trang 159 sách bài tập toán 9. Độ dài cạnh của tam giác đều nội tiếp đường tròn (O; R) bằng:
Bài 2.2 phần bài tập bổ sung trang 160 SBT toán 9 tập 1
Giải bài 2.2 phần bài tập bổ sung trang 160 sách bài tập toán 9. Cho đường tròn (O; 2cm). Vẽ hai dây AB và CD vuông góc với nhau. Tính diện tích lớn nhất của tứ giác ABCD.
Bài 2.3 phần bài tập bổ sung trang 160 SBT toán 9 tập 1
Giải bài 2.3 phần bài tập bổ sung trang 160 sách bài tập toán 9. Cho đường tròn (O; R), dây AB khác đường kính. Vẽ về hai phía của AB các dây AC, AD. Gọi H và K theo thứ tự là chân các đường vuông góc kẻ từ B và AC và AD. Chứng minh rằng: