-
PHẦN ĐẠI SỐ - SBT TOÁN 9 TẬP 1
-
CHƯƠNG 1: CĂN BẬC HAI. CĂN BẬC BA
- Bài 1. Căn bậc hai
- Bài 2. Căn thức bậc hai và hằng đẳng thức
- Bài 3. Liên hệ giữa phép nhân và phép khai phương
- Bài 4. Liên hệ giữa phép chia và phép khai phương
- Bài 5. Bảng căn bậc hai
- Bài 6. Biến đổi đơn giản biểu thức chứa căn thức bậc hai
- Bài 7. Biến đổi đơn giản biểu thức chứa căn thức bậc hai
- Bài 8. Rút gọn biểu thức chứa căn thức bậc hai
- Bài 9. Căn bậc ba
- Ôn tập chương 1 - Căn bậc hai. Căn bậc ba
-
CHƯƠNG 2: HÀM SỐ BẬC NHẤT
-
-
PHẦN HÌNH HỌC - SBT TOÁN 9 TẬP 1
-
CHƯƠNG 1: HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
-
CHƯƠNG 2: ĐƯỜNG TRÒN
- Bài 1. Sự xác định đường tròn. Tính chất đối xứng của đường tròn
- Bài 2. Đường kính và dây của đường tròn
- Bài 3. Liên hệ giữa dây và khoảng cách từ tâm đến dây
- Bài 4. Vị trí tương đối của đường thẳng và đường tròn
- Bài 5. Dấu hiệu nhận biết tiếp tuyến của đường tròn
- Bài 6. Tính chất của hai tiếp tuyến cắt nhau
- Bài 7. Vị trí tương đối của hai đường tròn
- Bài 8. Vị trí tương đối của hai đường tròn (tiếp theo)
- Ôn tập chương 2 - Đường tròn
-
-
PHẦN ĐẠI SỐ - SBT TOÁN 9 TẬP 2
-
CHƯƠNG 3: HỆ HAI PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
-
CHƯƠNG 4: HÀM SỐ y=ax^2 (a ≠ 0). PHƯƠNG TRÌNH BẬC HAI MỘT ẨN
- Bài 1. Hàm số bậc hai y=ax^2 (a ≠ 0)
- Bài 2. Đồ thị của hàm số bậc hai
- Bài 3. Phương trình bậc hai một ẩn
- Bài 4. Công thức nghiệm của phương trình bậc hai
- Bài 5. Công thức nghiệm thu gọn
- Bài 6. Hệ thức Vi-ét và ứng dụng
- Bài 7. Phương trình quy về phương trình bậc hai
- Bài 8. Giải bài toán bằng cách lập phương trình
- Bài tập ôn chương 4 - Hàm số y=ax^2 (a ≠ 0). Phương trình bậc hai một ẩn
-
-
PHẦN HÌNH HỌC - SBT TOÁN 9 TẬP 2
-
CHƯƠNG 3: GÓC VỚI ĐƯỜNG TRÒN
- Bài 1. Góc ở tâm. Số đo cung
- Bài 2. Liên hệ giữa cung và dây
- Bài 3. Góc nội tiếp
- Bài 4. Góc tạo bởi tia tiếp tuyến và dây cung
- Bài 5. Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh bên ngoài đường tròn
- Bài 6. Cung chứa góc
- Bài 7. Tứ giác nội tiếp
- Bài 8. Đường tròn ngoại tiếp. Đường tròn nội tiếp
- Bài 9. Độ dài đường tròn, cung tròn
- Bài 10. Diện tích hình tròn, hình quạt tròn
- Bài tập ôn chương 3 - Góc với đường tròn
-
CHƯƠNG 4: HÌNH TRỤ - HÌNH NÓN – HÌNH CẦU
-
BÀI TẬP ÔN TẬP CUỐI NĂM
-
Giải SBT đại số, hình học toán lớp 9 tập 1, tập 2
Bài 1. Sự xác định đường tròn. Tính chất đối xứng của đ..
Bài 14* trang 158 SBT toán 9 tập 1
Giải bài 14* trang 158 sách bài tập toán 9. Cho đường tròn (O) và hai điểm A, B nằm bên ngoài đường tròn. Dựng đường kính COD sao cho AC = BD...
Đề bài
Cho đường tròn (O) và hai điểm \(A, B\) nằm bên ngoài đường tròn. Dựng đường kính \(COD\) sao cho \(AC = BD.\)
Phương pháp giải - Xem chi tiết
Sử dụng tính chất đường trung trực của đoạn thẳng.
Các bước dựng hình:
+ Dựng điểm \(A'\) đối xứng với \(A\) qua \(O.\)
+ Dựng đường trung trực d của \(A'B\), cắt (O) tại \(D\).
+ Dựng đường kính \(COD\).
Lời giải chi tiết
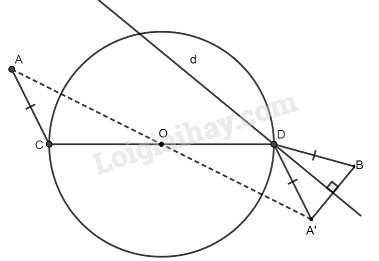
* Cách dựng
− Dựng \(A'\) đối xứng với \(A\) qua tâm \(O\) của đường tròn.
− Dựng đường thẳng \(d\) là đường trung trực của \(A’B.\)
− Gọi giao điểm của đường thẳng \(d\) và đường tròn (O) là \(D.\)
− Dựng đường kính \(COD.\)
* Chứng minh
Ta có: \(OA = OA’\) (do A và A' đối xứng nhau qua O) và \(OD = OC\) (do C, D cùng thuộc đường tròn (O))
Suy ra tứ giác \(ACA’D\) là hình bình hành (vì có hai đường chéo AA' và CD giao nhau tại trung điểm O của mỗi đường)
Suy ra: \(AC = A’D\) (tính chất hình bình hành)
Lại có: \(A’D = DB\) (tính chất đường trung trực)
Suy ra: \(AC = BD.\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 1.1 phần bài tập bổ sung trang 158 SBT toán 9 tập 1
- Bài 1.2 phần bài tập bổ sung trang 158 SBT toán 9 tập 1
- Bài 1.3 phần bài tập bổ sung trang 158 SBT toán 9 tập 1
- Bài 13* trang 158 SBT toán 9 tập 1
- Bài 12 trang 158 SBT toán 9 tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
