-
PHẦN ĐẠI SỐ - SBT TOÁN 9 TẬP 1
-
CHƯƠNG 1: CĂN BẬC HAI. CĂN BẬC BA
- Bài 1. Căn bậc hai
- Bài 2. Căn thức bậc hai và hằng đẳng thức
- Bài 3. Liên hệ giữa phép nhân và phép khai phương
- Bài 4. Liên hệ giữa phép chia và phép khai phương
- Bài 5. Bảng căn bậc hai
- Bài 6. Biến đổi đơn giản biểu thức chứa căn thức bậc hai
- Bài 7. Biến đổi đơn giản biểu thức chứa căn thức bậc hai
- Bài 8. Rút gọn biểu thức chứa căn thức bậc hai
- Bài 9. Căn bậc ba
- Ôn tập chương 1 - Căn bậc hai. Căn bậc ba
-
CHƯƠNG 2: HÀM SỐ BẬC NHẤT
-
-
PHẦN HÌNH HỌC - SBT TOÁN 9 TẬP 1
-
CHƯƠNG 1: HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
-
CHƯƠNG 2: ĐƯỜNG TRÒN
- Bài 1. Sự xác định đường tròn. Tính chất đối xứng của đường tròn
- Bài 2. Đường kính và dây của đường tròn
- Bài 3. Liên hệ giữa dây và khoảng cách từ tâm đến dây
- Bài 4. Vị trí tương đối của đường thẳng và đường tròn
- Bài 5. Dấu hiệu nhận biết tiếp tuyến của đường tròn
- Bài 6. Tính chất của hai tiếp tuyến cắt nhau
- Bài 7. Vị trí tương đối của hai đường tròn
- Bài 8. Vị trí tương đối của hai đường tròn (tiếp theo)
- Ôn tập chương 2 - Đường tròn
-
-
PHẦN ĐẠI SỐ - SBT TOÁN 9 TẬP 2
-
CHƯƠNG 3: HỆ HAI PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
-
CHƯƠNG 4: HÀM SỐ y=ax^2 (a ≠ 0). PHƯƠNG TRÌNH BẬC HAI MỘT ẨN
- Bài 1. Hàm số bậc hai y=ax^2 (a ≠ 0)
- Bài 2. Đồ thị của hàm số bậc hai
- Bài 3. Phương trình bậc hai một ẩn
- Bài 4. Công thức nghiệm của phương trình bậc hai
- Bài 5. Công thức nghiệm thu gọn
- Bài 6. Hệ thức Vi-ét và ứng dụng
- Bài 7. Phương trình quy về phương trình bậc hai
- Bài 8. Giải bài toán bằng cách lập phương trình
- Bài tập ôn chương 4 - Hàm số y=ax^2 (a ≠ 0). Phương trình bậc hai một ẩn
-
-
PHẦN HÌNH HỌC - SBT TOÁN 9 TẬP 2
-
CHƯƠNG 3: GÓC VỚI ĐƯỜNG TRÒN
- Bài 1. Góc ở tâm. Số đo cung
- Bài 2. Liên hệ giữa cung và dây
- Bài 3. Góc nội tiếp
- Bài 4. Góc tạo bởi tia tiếp tuyến và dây cung
- Bài 5. Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh bên ngoài đường tròn
- Bài 6. Cung chứa góc
- Bài 7. Tứ giác nội tiếp
- Bài 8. Đường tròn ngoại tiếp. Đường tròn nội tiếp
- Bài 9. Độ dài đường tròn, cung tròn
- Bài 10. Diện tích hình tròn, hình quạt tròn
- Bài tập ôn chương 3 - Góc với đường tròn
-
CHƯƠNG 4: HÌNH TRỤ - HÌNH NÓN – HÌNH CẦU
-
BÀI TẬP ÔN TẬP CUỐI NĂM
-
Bài 13 trang 63 SBT toán 9 tập 1
Giải bài 13 trang 63 sách bài tập toán 9. Tìm khoảng cách giữa hai điểm trên mặt phẳng tọa độ, biết rằng :..
Đề bài
Tìm khoảng cách giữa hai điểm trên mặt phẳng tọa độ , biết rằng :
a) A(1;1), B(5;4);
b) M(-2;2), N(3;5);
c) P(\(x_1; y_1\) ), Q(\(x_2; y_2\) )
Phương pháp giải - Xem chi tiết
+) Biểu diễn điểm \(M({x_0};{y_0})\) trên mặt phẳng tọa độ.
+) Tính khoảng cách:
Áp dụng định lí Pytago và tam giác ABC vuông tại A: \(A{B^2} + A{C^2} = B{C^2}\)
Lời giải chi tiết
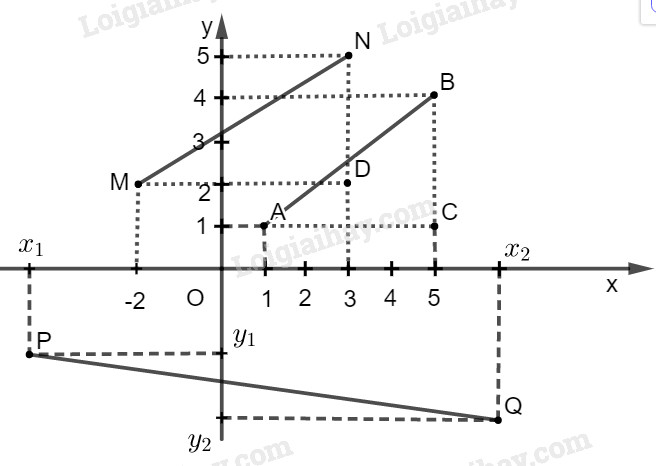
a) Lấy thêm điểm \(C(5;1)\) như hình vẽ.
Ta có :
Áp dụng Pytago vào tam giác ABC ta có:
\(\eqalign{
& A{B^2} = A{C^2} + B{C^2} \cr
& = {\left( {5 - 1} \right)^2} + {\left( {4 - 1} \right)^2} \cr
& = 16 + 9 = 25 \cr} \)
\(AB = \sqrt {25} = 5\)
Cách 2: \(AB = \sqrt {{{\left( {{5} - {1}} \right)}^2} + {{\left( {{4} - {1}} \right)}^2}} \) = \(\sqrt {25} = 5\)
b) Lấy thêm điểm \(D(3;2)\) như hình vẽ.
Ta có :
Áp dụng Pytago vào tam giác MND ta có:
\(\eqalign{
& M{N^2} = M{D^2} + N{D^2} \cr
& = {\left( {3 + 2} \right)^2} + {\left( {5 -2} \right)^2} \cr
& = 25 + 9 = 34 \cr} \)
\(MN = \sqrt {34} \approx 5,83\)
Cách 2: \(CD = \sqrt {{{\left( {{3} - {-2}} \right)}^2} + {{\left( {{5} - {2}} \right)}^2}} \) = \(\sqrt {34}\approx 5,83\)
c) Ta có :
\(PQ = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 2.1 phần bài tập bổ sung trang 63 SBT toán 9 tập 1
- Bài 2.2 phần bài tập bổ sung trang 63 SBT toán 9 tập 1
- Bài 2.3 phần bài tập bổ sung trang 63 SBT toán 9 tập 1
- Bài 2.4 phần bài tập bổ sung trang 63 SBT toán 9 tập 1
- Bài 12 trang 62 SBT toán 9 tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
