-
CHƯƠNG 1: PHÉP NHÂN VÀ PHÉP CHIA ĐA THỨC
-
Chủ đề 1 : Phép nhân đa thức – Hằng đẳng thức đáng nhớ
-
Chủ đề 2 : Phân tích đa thức thành nhân tử
- 1. Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
- 2. Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
- 3. Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
- 4. Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp
- Bài tập - Chủ đề 2 : Phân tích đa thức thành nhân tử
- Luyện tập - Chủ đề 2 : Phân tích đa thức thành nhân tử
-
Chủ đề 3: Phép chia đa thức
-
Ôn tập chương 1 - Phép nhân và phép chia đa thức
-
-
CHƯƠNG 2: PHÂN THỨC ĐẠI SỐ
-
CHƯƠNG 1. TỨ GIÁC
-
Chủ đề 1 : Tứ giác – Hình thang
-
Chủ đề 2 : Hình bình hành – Hình chữ nhật – Hình thoi – Hình vuông
- 1. Đối xứng trục
- 2. Hình bình hành
- 3. Đối xứng tâm
- 4. Hình chữ nhật
- 5. Tập hợp các điểm cách đều một đường thẳng cho trước
- 6. Hình thoi
- 7. Hình vuông
- Bài tập - Chủ đề 2 : Hình bình hành – Hình chữ nhật – Hình thoi – Hình vuông
- Luyện tập - Chủ đề 2 : Hình bình hành – Hình chữ nhật – Hình thoi – Hình vuông
-
Ôn tập chương 1 - Tứ giác
-
-
CHƯƠNG 2. ĐA GIÁC. DIỆN TÍCH ĐA GIÁC
-
CHƯƠNG 3 : PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN – GIẢI BÀI TOÁN BẰNG CÁCH LẬP PHƯƠNG TRÌNH
-
CHƯƠNG 4. BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
-
CHƯƠNG 3. TAM GIÁC ĐỒNG DẠNG
-
Chủ đề 1 : Định lí Thales
-
Chủ đề 2 : Tam giác đồng dạng và ứng dụng
- 1. Khái niệm hai tam giác đồng dạng
- 2. Trường hợp đồng dạng thứ nhất (c.c.c)
- 3. Trường hợp đồng dạng thứ hai (c.g.c)
- 4. Trường hợp đồng dạng thứ ba (g.g)
- 5. Các trường hợp đồng dạng của tam giác vuông
- 6. Ứng dụng thực tế của tam giác đồng dạng
- Bài tập - Chủ đề 2 : Tam giác đồng dạng và ứng dụng
- Luyện tập - Chủ đề 2 : Tam giác đồng dạng và ứng dụng
-
-
CHƯƠNG 4 : HÌNH LĂNG TRỤ ĐỨNG – HÌNH CHÓP ĐỀU
-
ÔN TẬP CUỐI NĂM - TÀI LIỆU DẠY-HỌC TOÁN 8
Giải bài tập Tài liệu Dạy - học Toán lớp 8, Phát triển tư duy đột phá trong dạy học Toán 8
Bài tập - Chủ đề 1 : Định lí Thales
Bài tập 4 trang 68 Tài liệu dạy – học Toán 8 tập 2
Giải bài tập Tìm x, y trong các hình vẽ sau:
Đề bài
Tìm x, y trong các hình vẽ sau:
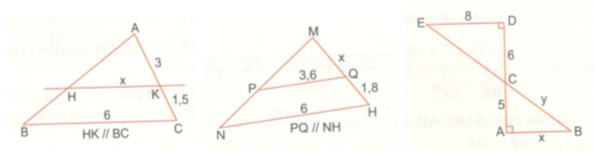
Lời giải chi tiết
• Xét ∆ABC có HK // BC \( \Rightarrow \dfrac{{HK}}{{BC}} = \dfrac{{AK}}{{AC}}\) (định lí Thales)
Mà \(HK = x,BC = 6,AK = 3,\) \(\,AC = AK + KC = 3 + 1,5 = 4,5\)
Nên \(\dfrac{x}{6} = \dfrac{3}{{4,5}} \Rightarrow x = \dfrac{{6.3}}{{4,5}} = 4 \Leftrightarrow x = 4\)
• Xét ∆MNH có PQ // NH \( \Rightarrow \dfrac{{MQ}}{{MH}} = \dfrac{{PQ}}{{NH}}\) (định lí Thales)
Mà \(MQ = x,MH = x + 1,8,PQ = 3,6,\)\(\,NH = 6 \Rightarrow \dfrac{x}{{x + 1,8}} = \dfrac{{3,6}}{6}\)
\(\eqalign{ & \Leftrightarrow 6x = (x + 1,8).3,6 \cr & \Leftrightarrow 6x = 3,6x + 6,48 \cr & \Leftrightarrow 2,4x = 6,48 \cr & \Leftrightarrow x = 2,7 \cr} \)
• Ta có
\(\left. \matrix{ ED \bot AD \hfill \cr AB \bot AD \hfill \cr} \right\} \Rightarrow ED//AB;\)
Xét ∆ECD vuông tại D, theo định lý Py-ta-go có \(E{C^2} = E{D^2} + C{D^2} = {6^2} + {8^2} \)
\(\Rightarrow EC = 10\)
Xét ∆ABC có \(ED//AB \Rightarrow \dfrac{{AB}}{{ED}} = \dfrac{{BC}}{{EC}} = \dfrac{{AC}}{{CD}}\) (hệ quả định lý Thales)
Từ đó, suy ra:
\(\eqalign{ & {x \over 8} = {5 \over 6} \Rightarrow x = {{8.5} \over 6} \approx 6,67 \cr & {y \over {10}} = {5 \over 6} \Rightarrow y = {{10.5} \over 6} \approx 8,33 \cr} \)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài tập 5 trang 68 Tài liệu dạy – học Toán 8 tập 2
- Bài tập 6 trang 69 Tài liệu dạy – học Toán 8 tập 2
- Bài tập 7 trang 69 Tài liệu dạy – học Toán 8 tập 2
- Bài tập 8 trang 69 Tài liệu dạy – học Toán 8 tập 2
- Bài tập 9 trang 69 Tài liệu dạy – học Toán 8 tập 2
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
